円周角の定理の証明

円周角の定理とは

円周上にとる点の位置に関わりなく、円周角の大きさ C は対応する円弧を含む扇形の中心角の大きさ $\alpha$ のみに依存し、以下のように表わされる。

$\displaystyle C=\frac{\alpha}{2}$

すなわち $\displaystyle \alpha=2C$
これは円周角の定理として知られる。

ウィキペディアの執筆者，2020，「円周角」『ウィキペディア日本語版』，（2021年6月30日取得，https://ja.wikipedia.org/w/index.php?title=%E5%86%86%E5%91%A8%E8%A7%92&oldid=79241562）．

図で説明すると、下記のとおりです。

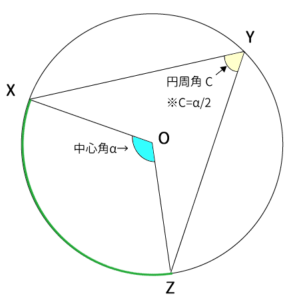
円周上に3点とると（$X$、$Y$、$Z$とする）、上のように$\angle XYZ$が作れます。これを弧$\stackrel{\huge\frown}{XZ}$に対する円周角といいます。ここでは、円周角$C$とします。

次に、円の中心$O$に対して、$\angle XOY$が作れます。これを弧$\stackrel{\huge\frown}{XZ}$に対する中心角といいます。ここでは中心角$\alpha$とします。

このとき、どのような3点に対しても、$\alpha = 2c$が成り立つ。これが円周角の定理です。

外接円

上図の円を$\bigtriangleup XYZ$の外接円といいます。

円周角の定理の証明

円周角は鋭角、直角、鈍角の3パターン考えられますので、それぞれを証明していきます。

円周角が鋭角（$0^{\circ}<\theta<90^{\circ}$）の場合

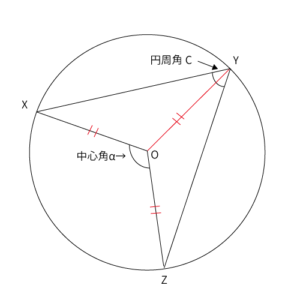
※外接円の半径をRとします

$OY$を引くと、$OX=OY=R$なので、$\bigtriangleup OXY$は2等辺三角形となります。同様に$OY=OZ=R$なので、$\bigtriangleup OYZ$も2等辺三角形となります。

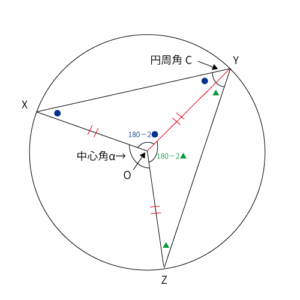
$\bigtriangleup OXY$、$\bigtriangleup OYZ$はともに2等辺三角形なので、$\color{blue} \angle OXY=\angle XYO=●$、$\color{green} \angle OYZ=\angle YZO=▲$となります。

ここで、$\color{blue} \angle XYO=●$、$\color{green} \angle OYZ=▲$と置いているので、円周角$C=\color{blue} ●\color{black} +\color{green} ▲\color{black}$となります。

三角形の角度の和は$180^{\circ}$なので、$\color{blue} \angle YOX=180-2●$、$\color{green} \angle ZOY=180-2▲$となります。

よって、中心角$\alpha$は$360^{\circ}$からこれら2つの角度を引いたものなので、
$\alpha=360-\color{blue} (180-2●)\color{black} -\color{green} (180-2▲)$

中心角$\alpha=2(\color{blue} ●\color{black} +\color{green} ▲\color{black})$となります。

円周角$C=\color{blue} ●\color{black} +\color{green} ▲\color{black}$なので、中心角$\alpha=2(\color{blue} ●\color{black} +\color{green} ▲\color{black})=2C$

従って、円周角が鋭角のとき、円周角の定理が成り立つことを証明できました。

円周角が直角（$\theta=90^{\circ}$）の場合

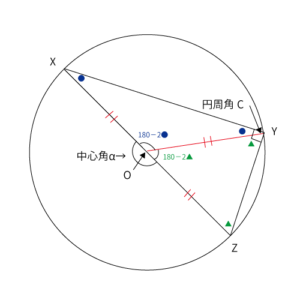
上図のとおり、鋭角と全く同じです。よって、鋭角と同じ流れで中心角$\alpha=2(\color{blue} ●\color{black} +\color{green} ▲\color{black})=2C$を証明できます。では、ざっと書きます。

※外接円の半径をRとします

$OY$を引くと、$\bigtriangleup OXY$と$\bigtriangleup OYZ$はともに2等辺三角形となるので、$\color{blue} \angle OXY=\angle XYO=●$、$\color{green} \angle OYZ=\angle YZO=▲$となります。

また、円周角$C=\color{blue} ●\color{black} +\color{green} ▲\color{black}$となります。

三角形の角度の和は$180^{\circ}$なので、$\color{blue} \angle YOX=180-2●$、$\color{green} \angle ZOY=180-2▲$となります。

円周角$C=\color{blue} ●\color{black} +\color{green} ▲\color{black}$なので、中心角$\alpha=2(\color{blue} ●\color{black} +\color{green} ▲\color{black})=2C$

従って、円周角が直角のときも、円周角の定理が成り立つことを証明できました。

円周角が直角のときの性質

円周角が直角の場合、円周角の定理（$\alpha=2C$）が成り立つことが分かりました。

円周角が直角なので、中心角はその2倍の$180^{\circ}$となります。

弧$\stackrel{\huge\frown}{XZ}$に対する中心角が$180^{\circ}$、つまり、弧$\stackrel{\huge\frown}{XZ}$は外接円の半円になります。ということは、$XZ$は外接円を真っ二つに切る直線なので、$XZ$は外接円の直径であることが分かりました。

言い換えると、直角三角形$XYZ$の斜辺XZは$\bigtriangleup XYZ$の外接円の直径である。

これは是非覚えておきたい性質ですね。

円周角が鈍角（$90^{\circ}<\theta<180^{\circ}$）の場合

上図のとおり、鈍角の場合も同様でした。よって、鋭角・直角と同じ流れで中心角$\alpha=2(\color{blue} ●\color{black} +\color{green} ▲\color{black})=2C$を証明できます。では、ざっと書きます。

※外接円の半径をRとします

$OY$を引くと、$\bigtriangleup OXY$と$\bigtriangleup OYZ$はともに2等辺三角形となるので、$\color{blue} \angle OXY=\angle XYO=●$、$\color{green} \angle OYZ=\angle YZO=▲$となります。

また、円周角$C=\color{blue} ●\color{black} +\color{green} ▲\color{black}$となります。

三角形の角度の和は$180^{\circ}$なので、$\color{blue} \angle YOX=180-2●$、$\color{green} \angle ZOY=180-2▲$となります。

円周角$C=\color{blue} ●\color{black} +\color{green} ▲\color{black}$なので、中心角$\alpha=2(\color{blue} ●\color{black} +\color{green} ▲\color{black})=2C$

従って、円周角が鈍角のときも、円周角の定理が成り立つことを証明できました。

以上、円周角が鋭角、直角、鈍角の全パターンで円周角の定理が成り立つことが証明できました。

Q.E.D.

スポンサーリンク

キーワード

気になる人は調べてみてね。

円周角の定理、円周角、中心角、外接円、Q.E.D.