
すっかり忘れていましたが、円に内接する四角形の性質です。
「円に内接する四角形の内角はその内角の対角の外角に等しい」です。図を描いて円周角の定理を使えば簡単に証明できますので見ていきましょう。
円に内接する四角形
↓が円に内接する四角形です。
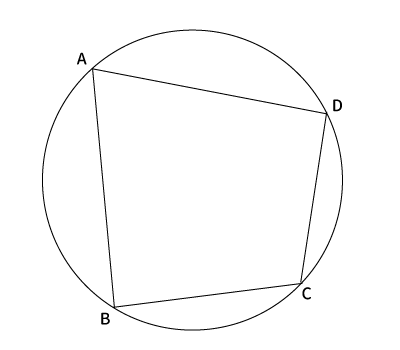
「円に内接する四角形の内角はその内角の対角の外角に等しい」とは?
図を見ると分かりやすいので、下図をみてください。

赤い2角が等しくなります。
まずはざっくりとした証明の流れです。
証明のざっくりとした流れ
$\angle DAB$(※$\angle A$)に対しての流れです。
まるっと下図に要素が詰まっています。
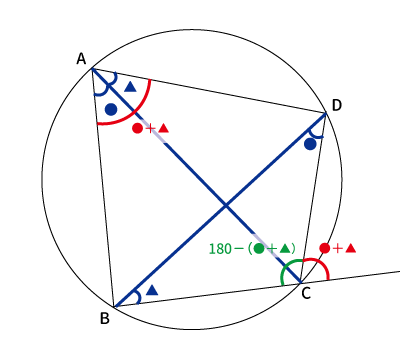
円周角の定理より、青い●が同じ角度になる、同様に青い▲も同じ角度。
※円周角については「【円周角の定理より】1つの円弧に対する円周角はどの円周角も等しくなる」をご覧ください。
すると、三角形の内角の和は$180^{\circ}$なので$\bigtriangleup BCD$の内角$\angle BCD$は$180-(●+▲)$となる。よって、この内角の外角は$180-\{180-(●+▲)\}=●+▲$。なんとこれは$\angle BAD$(※$\angle A$)と同じですね。
他の内角も全く同じ方法です。
それでは、1つずつ詳しく見ていきましょう。
$\angle A=\angle C$の外角
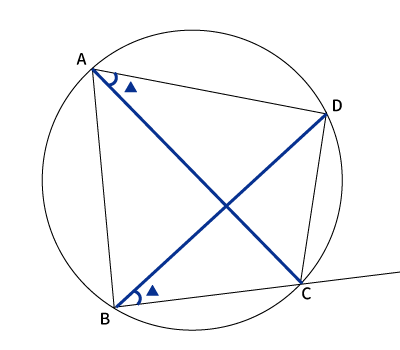
まず、四角形$ABCD$の対角線$AC$、$BD$を2本引きます。

ここで円周角の定理より、同じ円弧に対して円周角は同じになるので、2か所角度が同じことが分かります。
1つ目が$\angle BAC= \angle BDC$です。

2つ目が$\angle CAD= \angle CBD$です。
まとめると、下図のようになり、また、$\angle DAB$は●と▲を足すことは自明なので、$\angle DAB=●+▲$も書き込みました。
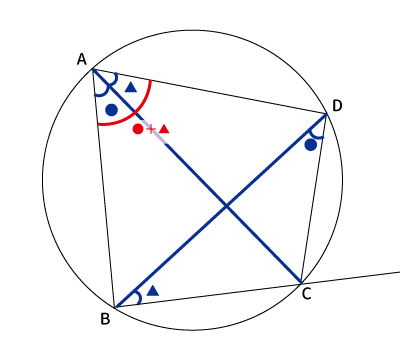
続いて$\bigtriangleup BCD$をみると、2角判明していて、●と▲でした。三角形の内角の和は$180^{\circ}$なので、$\angle C$が$180-(●+▲)$となります。
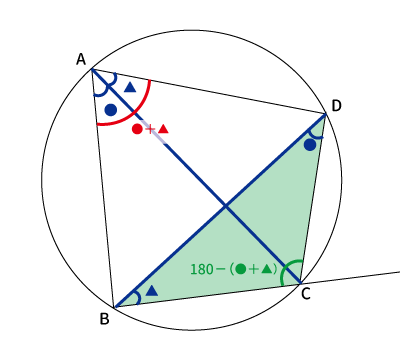
最後に$\angle C$が$\angle C$が$180-(●+▲)$なので、$\angle C$の外角は$180-(180-(●+▲))$です。よって、$\angle C$の外角は$●+▲$です。
以上より、\$angle A=●+▲$、$\angle C$の外角は$●+▲$となりました。従って、「円に内接する四角形の内角はその内角の対角の外角に等しい」を証明できました。
以上、証明終わり。
その他の内角
その他の内角に関しても同様の手順で内角とその内角の対角の外角が等しいことが求められます。
それぞれどことどこの角度が等しいかをまとめた画像を参考に載せておきますので、自分で求める時間がない場合は参考にしてみてください。
$\angle D=\angle B$の外角
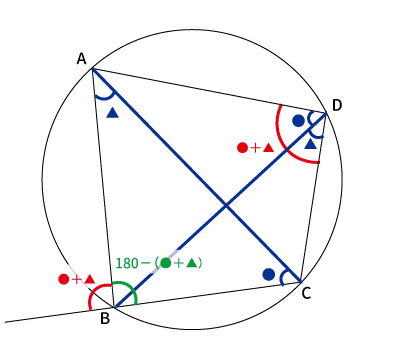
$\angle C=\angle A$の外角
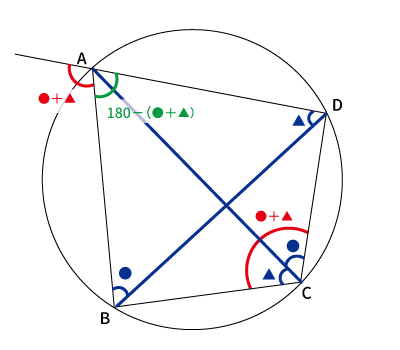
$\angle B=\angle D$の外角

キーワード
気になる人は調べてみてね。
円に内接する四角形、内接、円周角の定理、対角、内角




