
三角比の相互関係の1つ$\sin^2 \theta + \cos^2 \theta = 1$は単位円を描くと簡単に理解することができます。
単位円
単位円とは下図のように原点$O$を中心とする半径1の円のことです。
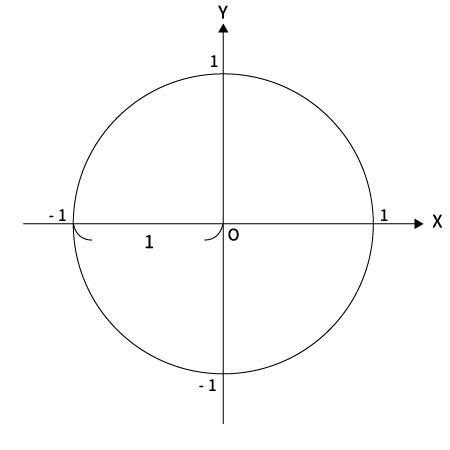
単位円について詳しくは下記をご覧ください。
単位円とは原点を中心とする半径1の円のことです。 この単位円を使うことで、$sin$、$cos$の値を簡単な形で表すことができます。三角比を考える上で非常に便利なツールなので覚えておくことをオススメします。 単位円 …
単位円上の点$P$の座標が$(\cos \theta, \, \sin \theta)$
単位円の円周上に点$P$の座標が$(\cos \theta, \, \sin \theta)$と定義されています。詳しくは単位円のページを見てくださいね。
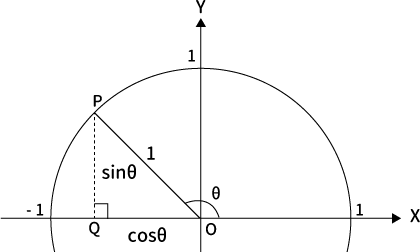
三平方の定理より$\sin^2 \theta + \cos^2 \theta = 1$を満たす
単位円の点$P(\cos \theta, \, \sin \theta)$より$\theta$がどのような角度の場合でも$\sin^2 \theta + \cos^2 \theta = 1$を満たすことが分かります。
それでは各パターンを確認してみましょう。
$0^{\circ} < \theta < 90^{\circ}$の場合
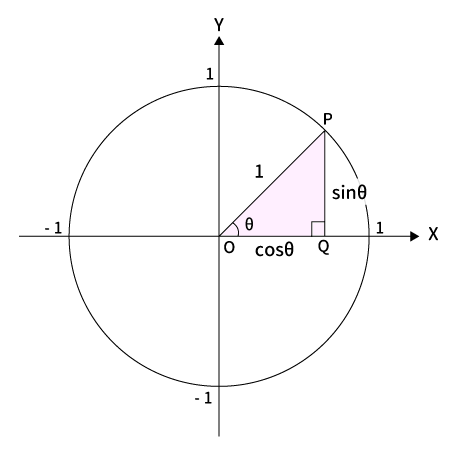
$\bigtriangleup OPQ$は直角三角形なので、三平方の定理より$\sin^2 \theta + \cos^2 \theta = 1$を満たします。
$90^{\circ} < \theta < 180^{\circ}$の場合
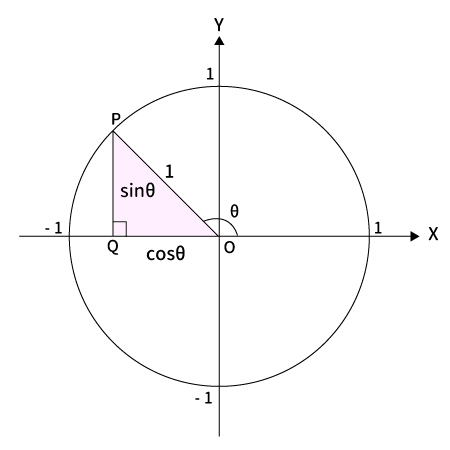
$\bigtriangleup OPQ$は直角三角形なので、三平方の定理より$\sin^2 \theta + \cos^2 \theta = 1$を満たします。
※2乗するのでプラスマイナスは関係ありません
$180^{\circ} < \theta < 270^{\circ}$の場合
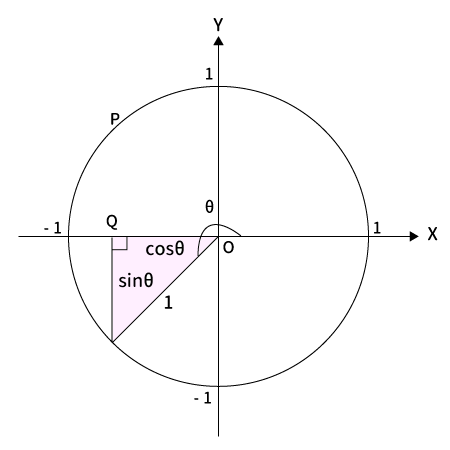
$\bigtriangleup OPQ$は直角三角形なので、三平方の定理より$\sin^2 \theta + \cos^2 \theta = 1$を満たします。
※2乗するのでプラスマイナスは関係ありません
$180^{\circ} < \theta < 270^{\circ}$の場合
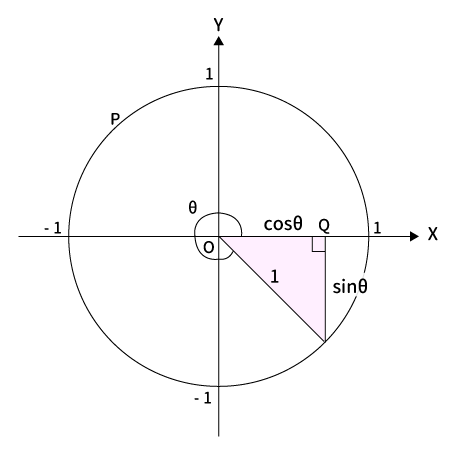
$\bigtriangleup OPQ$は直角三角形なので、三平方の定理より$\sin^2 \theta + \cos^2 \theta = 1$を満たします。
※2乗するのでプラスマイナスは関係ありません
$\theta$が$0^{\circ},\,90^{\circ},\,180^{\circ},\,270^{\circ}$のとき
$\theta$が$0,\,90,\,180,\,270$のときの座標は下記のとおりです。
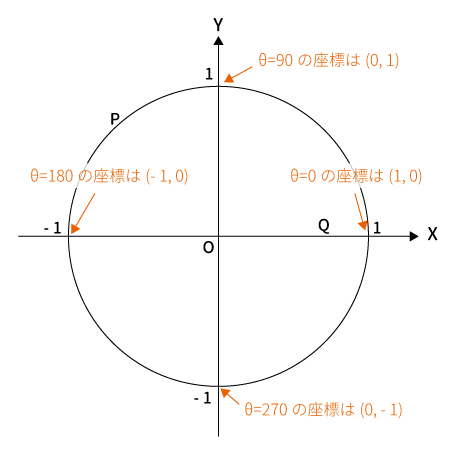
表にまとめると、下記のようになり、すべて$\sin^2 \theta + \cos^2 \theta = 1$を満たします。
| $\theta$ | $\cos \theta$ | $\sin \theta$ | $\sin^2 \theta + \cos^2 \theta$ |
|---|---|---|---|
| $0^{\circ}$ | 1 | 0 | 1 |
| $90^{\circ}$ | 0 | 1 | 1 |
| $180^{\circ}$ | -1 | 0 | 1 |
| $270^{\circ}$ | 0 | -1 | 1 |
まとめ
単位円を使うことで$\theta$が$0^{\circ}~360^{\circ}$の全パターンで$\sin^2 \theta + \cos^2 \theta = 1$を満たすことが確認できました。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
単位円、$\sin \theta$、$\cos \theta$、$\sin^2 \theta + \cos^2 \theta = 1$、三角比





