前編と同様に三角形を転がして三角関数の関係をチェックしていきたいと思います。
単位円と転がす三角形
前回と同様ですが、改めて確認しておきます。続けて読む方は飛ばしてくださいね。
単位円
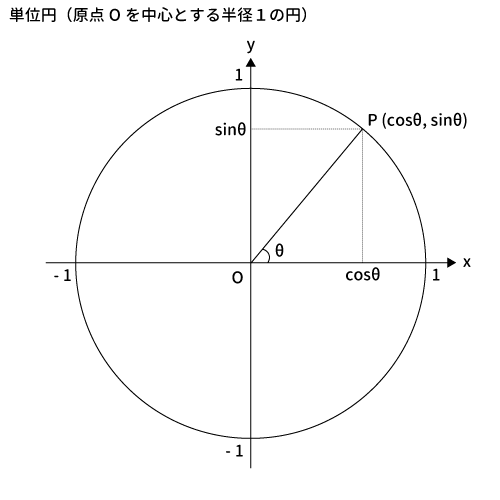
前回と同様、単位円の円周上に点$P$をとるとき、その座標を$(1, \, 0 )$からの角度$\theta$を用いて、$P$の座標を$(\cos\theta, \, \sin\theta )$とします。
転がす三角形
こちらも前回と同様、点$P$から$x$軸に下ろした垂線と$x$軸との交点を$A$とします。このとき、単位円の円周上の点$P$、原点$O$、点$A$の3点でできる$\bigtriangleup OAP$を転がして三角関数の関係を見ていきたいと思います。

三角形の各辺の長さと$\tan \theta$の値は下記の通りです。詳細が気になる方は前編をご覧ください。
$OA=\cos\theta$
$AP=\sin\theta$
$OP=1$
$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$
得られる関係式
$\cos(-\theta)=\cos\theta$
$\sin(-\theta)=-\sin\theta$
$\displaystyle \tan(-\theta) = -\tan\theta$
$\cos(90 ^{\circ}-\theta)=\sin\theta$
$\sin(90 ^{\circ}-\theta)=\cos\theta$
$\displaystyle \tan(90 ^{\circ}-\theta) = \frac{1}{\tan\theta}$
$\cos(180^{\circ}-\theta)=-\cos\theta$
$\sin(180^{\circ}-\theta)=\sin\theta$
$\displaystyle \tan(180^{\circ}-\theta) = -\tan\theta$
$\cos(270^{\circ}-\theta)=-\sin\theta$
$\sin(270^{\circ}-\theta)=-\cos\theta$
$\displaystyle \tan(270^{\circ}-\theta) = \frac{1}{\tan\theta}$
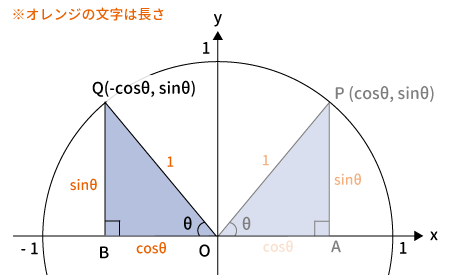
$x$座標を軸に回転($-\theta$)
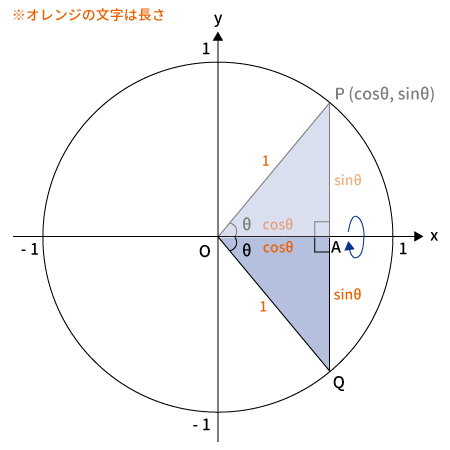
上図のように$\bigtriangleup OAP$を$x$座標を軸に回転させた後の点を$Q$とします。
※点$A$は共通
Qの座標
$Q$は$\theta$を$-\theta$となるように回転させたものなので、$Q$の座標は$(\cos(-\theta), \, \sin(-\theta))$です。
※$x$座標は$\cos$、$y$座標は$\sin$となります。詳細は「単位円とは?」をご覧ください
また、$\displaystyle \tan (-\theta) = \frac{\sin (-\theta)}{\cos (-\theta)}$です。
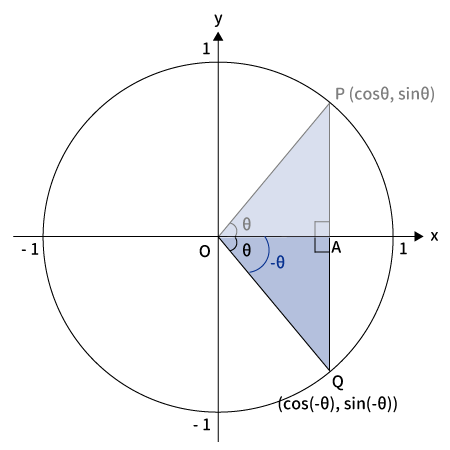
$\bigtriangleup OAQ$の各辺の長さ
回転させても三角形の各辺の長さは変わらないので、下記が成り立ちます。
$OA=\cos\theta$
$AQ=\sin\theta$
$OQ=1$
各辺の長さからも$Q$の座標を求める
$\bigtriangleup OAQ$の各辺の長さからも$Q$の座標を求めることができます。
下図を見てわかる通り、$Q$の$x$座標は$OA$、$y$座標は$-AQ$なので、$Q$の座標は$(\cos\theta, \, -\sin\theta)$となります。
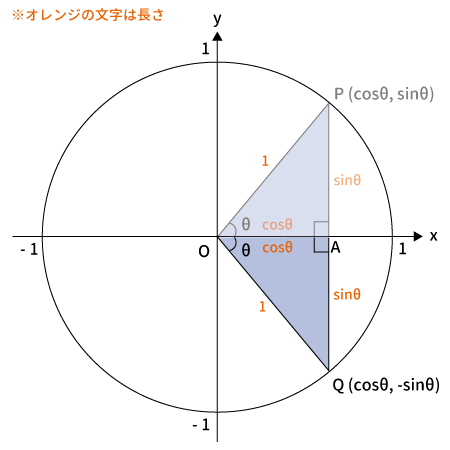
$Q$の座標$(\cos(-\theta), \, \sin(-\theta))$$=(\cos\theta, \, -\sin\theta)$
上記より$Q$の座標は$(\cos(-\theta), \, \sin(-\theta))$と$(\cos\theta, \, -\sin\theta)$と2通りの方法で表せたので、$x$、$y$座標同士がそれぞれ等しいということになります。
よって、
$\cos(-\theta)=\cos\theta$
$\sin(-\theta)=-\sin\theta$
$\tan (-\theta)$
$\displaystyle \tan (-\theta) = \frac{\sin (-\theta)}{\cos (-\theta)}$なので、上記2つを代入すると、
$\displaystyle \tan(-\theta) = \frac{-\sin\theta}{\cos\theta}$
さらに、$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$を代入すると、
$\displaystyle \tan(-\theta) = -\tan\theta$
$-\theta$と$\theta$の関係式
$\cos(-\theta)=\cos\theta$
$\sin(-\theta)=-\sin\theta$
$\displaystyle \tan(-\theta) = -\tan\theta$
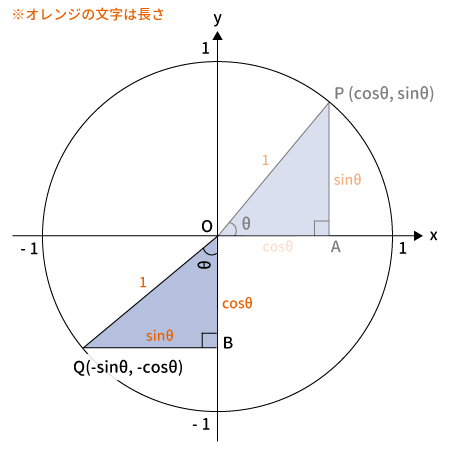
$-\theta$を$90 ^{\circ}$回転($90 ^{\circ}-\theta$)
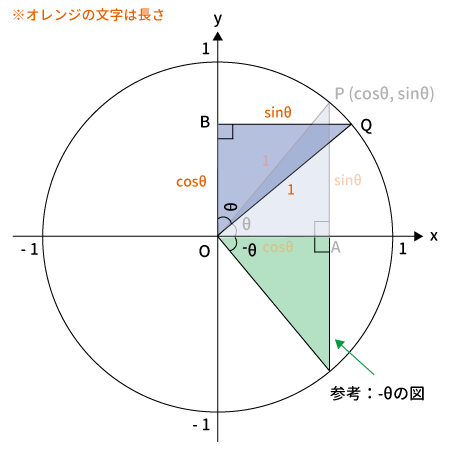
上図のように$-\theta$の三角形を$90 ^{\circ}$回転させた後の点を$Q$、$B$とします。
Qの座標
$Q$は$-\theta$を$90 ^{\circ}$回転させたものなので、$Q$の座標は$(\cos(90 ^{\circ}-\theta), \, \sin(90 ^{\circ}-\theta))$です。
※$x$座標は$\cos$、$y$座標は$\sin$となります。詳細は「単位円とは?」をご覧ください
また、$\displaystyle \tan (90 ^{\circ}-\theta) = \frac{\sin (90 ^{\circ}-\theta)}{\cos (90 ^{\circ}-\theta)}$です。
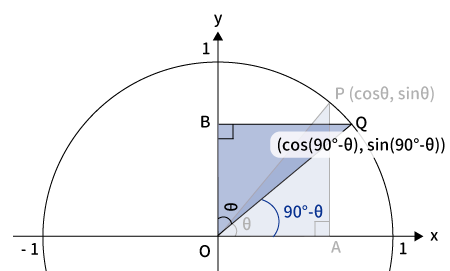
$\bigtriangleup OBQ$の各辺の長さ
回転させても三角形の各辺の長さは変わらないので、下記が成り立ちます。
$OB=\cos\theta$
$BQ=\sin\theta$
$OQ=1$
各辺の長さからも$Q$の座標を求める
$\bigtriangleup OBQ$の各辺の長さからも$Q$の座標を求めることができます。
下図を見てわかる通り、$Q$の$x$座標は$BQ$、$y$座標は$OB$なので、$Q$の座標は$(\sin\theta, \, \cos\theta)$となります。
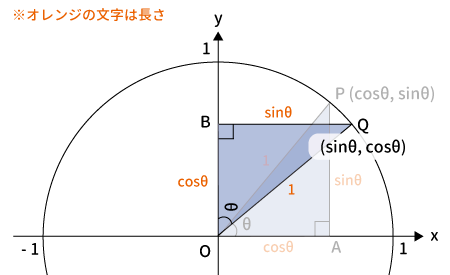
$Q$の座標$(\cos(90 ^{\circ}-\theta), \, \sin(90 ^{\circ}-\theta))$$=(\sin\theta, \, \cos\theta)$
上記より$Q$の座標は$(\cos(90 ^{\circ}-\theta), \, \sin(90 ^{\circ}-\theta))$と$(\sin\theta, \, \cos\theta)$と2通りの方法で表せたので、$x$、$y$座標同士がそれぞれ等しいということになります。
よって、
$\cos(90 ^{\circ}-\theta)=\sin\theta$
$\sin(90 ^{\circ}-\theta)=\cos\theta$
$\tan (90 ^{\circ}-\theta)$
$\displaystyle \tan (90 ^{\circ}-\theta) = \frac{\sin (90 ^{\circ}-\theta)}{\cos (90 ^{\circ}-\theta)}$なので、上記2つを代入すると、
$\displaystyle \tan(90 ^{\circ}-\theta) = \frac{\cos\theta}{\sin\theta}$
さらに、$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$より、$\displaystyle \frac{\cos \theta}{\sin \theta} = \frac{1}{\tan\theta}$。これを代入すると、
$\displaystyle \tan(90 ^{\circ}-\theta) = \frac{1}{\tan\theta}$
$90 ^{\circ}-\theta$と$\theta$の関係式
$\cos(90 ^{\circ}-\theta)=\sin\theta$
$\sin(90 ^{\circ}-\theta)=\cos\theta$
$\displaystyle \tan(90 ^{\circ}-\theta) = \frac{1}{\tan\theta}$
$-\theta$を$180 ^{\circ}$回転($180 ^{\circ}-\theta$)
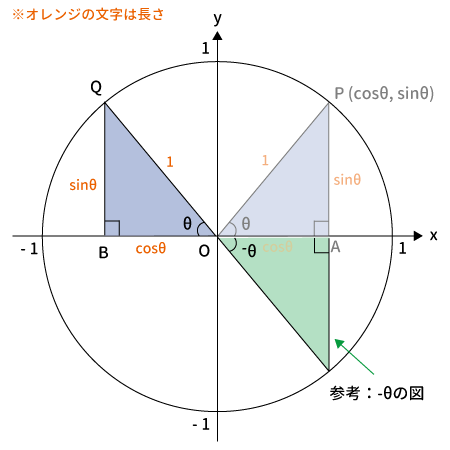
上図のように$-\theta$の三角形を$180 ^{\circ}$回転させた後の点を$Q$、$B$とします。
Qの座標
$Q$は$-\theta$を$180^{\circ}$回転させたものなので、$Q$の座標は$(\cos(180^{\circ}-\theta), \, \sin(180^{\circ}-\theta))$です。
※$x$座標は$\cos$、$y$座標は$\sin$となります。詳細は「単位円とは?」をご覧ください
また、$\displaystyle \tan (180^{\circ}-\theta) = \frac{\sin (180^{\circ}-\theta)}{\cos (180^{\circ}-\theta)}$です。

$\bigtriangleup OBQ$の各辺の長さ
回転させても三角形の各辺の長さは変わらないので、下記が成り立ちます。
$OB=\cos\theta$
$BQ=\sin\theta$
$OQ=1$
各辺の長さからも$Q$の座標を求める
$\bigtriangleup OBQ$の各辺の長さからも$Q$の座標を求めることができます。
下図を見てわかる通り、$Q$の$x$座標は$-OB$、$y$座標は$BQ$なので、$Q$の座標は$(-\cos\theta, \, \sin\theta)$となります。
$Q$の座標$(\cos(180^{\circ}-\theta), \, \sin(180^{\circ}-\theta))$$=(-\cos\theta, \, \sin\theta)$
上記より$Q$の座標は$(\cos(180^{\circ}-\theta), \, \sin(180^{\circ}-\theta))$と$(-\cos\theta, \, \sin\theta)$と2通りの方法で表せたので、$x$、$y$座標同士がそれぞれ等しいということになります。
よって、
$\cos(180^{\circ}-\theta)=-\cos\theta$
$\sin(180^{\circ}-\theta)=\sin\theta$
$\tan (180^{\circ}-\theta)$
$\displaystyle \tan (180^{\circ}-\theta) = \frac{\sin (180^{\circ}-\theta)}{\cos (180^{\circ}-\theta)}$なので、上記2つを代入すると、
$\displaystyle \tan(180^{\circ}-\theta) = \frac{\sin\theta}{-\cos\theta}$
さらに、$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$を代入すると、
$\displaystyle \tan(180^{\circ}-\theta) = -\tan\theta$
$180^{\circ}-\theta$と$\theta$の関係式
$\cos(180^{\circ}-\theta)=-\cos\theta$
$\sin(180^{\circ}-\theta)=\sin\theta$
$\displaystyle \tan(180^{\circ}-\theta) = -\tan\theta$
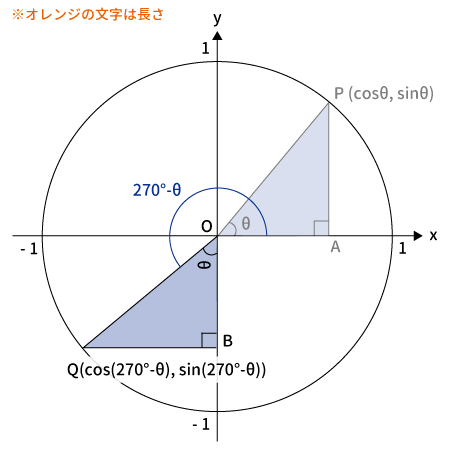
$-\theta$を$270 ^{\circ}$回転($270^{\circ}-\theta$)

上図のように$-\theta$の三角形を$270^{\circ}$回転させた後の点を$Q$、$B$とします。
Qの座標
$Q$は$-\theta$を$270^{\circ}$回転させたものなので、$Q$の座標は$(\cos(270^{\circ}-\theta), \, \sin(270^{\circ}-\theta))$です。
※$x$座標は$\cos$、$y$座標は$\sin$となります。詳細は「単位円とは?」をご覧ください
また、$\displaystyle \tan (270^{\circ}-\theta) = \frac{\sin (270^{\circ}-\theta)}{\cos (270^{\circ}-\theta)}$です。
$\bigtriangleup OBQ$の各辺の長さ
回転させても三角形の各辺の長さは変わらないので、下記が成り立ちます。
$OB=\cos\theta$
$BQ=\sin\theta$
$OQ=1$
各辺の長さからも$Q$の座標を求める
$\bigtriangleup OBQ$の各辺の長さからも$Q$の座標を求めることができます。
下図を見てわかる通り、$Q$の$x$座標は$-BQ$、$y$座標は$-OB$なので、$Q$の座標は$(-\sin\theta, \, -\cos\theta)$となります。
$Q$の座標$(\cos(270^{\circ}-\theta), \, \sin(270^{\circ}-\theta))$$=(-\sin\theta, \, -\cos\theta)$
上記より$Q$の座標は$(\cos(270^{\circ}-\theta), \, \sin(270^{\circ}-\theta))$と$(-\sin\theta, \, -\cos\theta)$と2通りの方法で表せたので、$x$、$y$座標同士がそれぞれ等しいということになります。
よって、
$\cos(270^{\circ}-\theta)=-\sin\theta$
$\sin(270^{\circ}-\theta)=-\cos\theta$
$\tan (270^{\circ}-\theta)$
$\displaystyle \tan (270^{\circ}-\theta) = \frac{\sin (270^{\circ}-\theta)}{\cos (270^{\circ}-\theta)}$なので、上記2つを代入すると、
$\displaystyle \tan(270^{\circ}-\theta) = \frac{-\cos\theta}{-\sin\theta}= \frac{\cos\theta}{\sin\theta}$
さらに、$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$より、$\displaystyle \frac{\cos \theta}{\sin \theta} = \frac{1}{\tan\theta}$。これを代入すると、
$\displaystyle \tan(270^{\circ}-\theta) = \frac{1}{\tan\theta}$
$270^{\circ}-\theta$と$\theta$の関係式
$\cos(270^{\circ}-\theta)=-\sin\theta$
$\sin(270^{\circ}-\theta)=-\cos\theta$
$\displaystyle \tan(270^{\circ}-\theta) = \frac{1}{\tan\theta}$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
まとめ
$x$座標が$cos$、$y$座標が$sin$さえ覚えておけば、後は単位円で考えればどの関係式も簡単に思い出せるかと思います。この細かい関係式を覚えるよりも他の公式を覚える方が効率的かもしれないですね。
キーワード
気になる人は調べてみてね。
三角関数、単位円、三平方の定理、$\sin \theta$、$\cos \theta$、$\tan \theta$