
「円周角の定理の証明」で円周角$C$が中心角$\alpha$の$\displaystyle \frac{1}{2}$ということを証明しました。
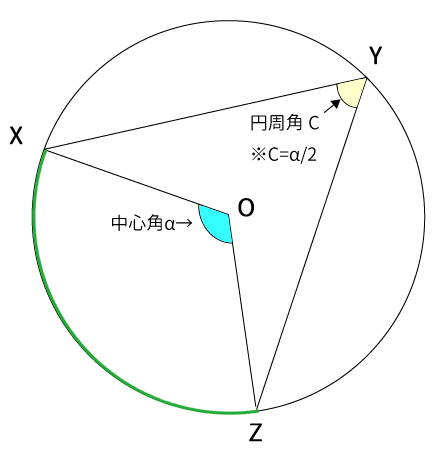
この証明のときに、この円周角の定理から分かる性質について触れていなかったので、チェックしておきます。
1つの円弧に対する円周角はどの円周角も等しくなる
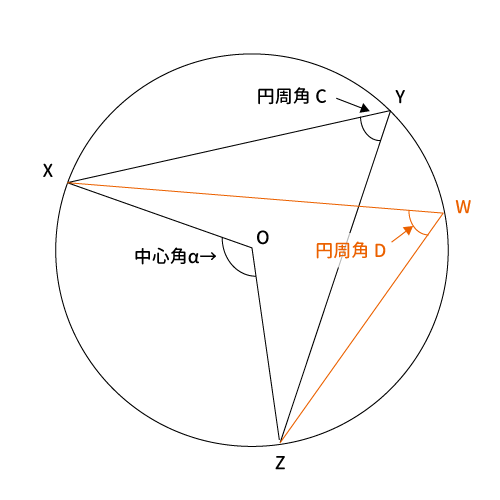
「1つの円弧に対する円周角はどの円周角も等しくなる」とは、下図の円周角$C$と円周角$D$が等しいという意味です。
図に合わせて言い直すと、「弧$\stackrel{\huge\frown}{XZ}$に対する任意の円周角$Y$、$W$は等しい」。
これは「円周角の定理」から簡単に導くことができます。
証明(実質、円周角の定理そのものですが…)
「円周角の定理」より、
$\displaystyle \angle C = \frac{\angle \alpha}{2}$
$\displaystyle \angle D = \frac{\angle \alpha}{2}$
よって、
$\angle C =\angle D$
使い方の例
問題
$\bigtriangleup XYZ$に対して$XZ=x$、$\angle XYZ = \beta$とする。また、$\bigtriangleup XYZ$の外接円の半径が$r$である。このとき、$\cos \angle \beta$を求めたい。
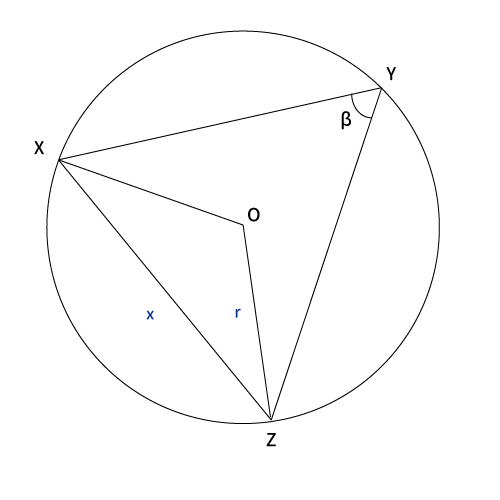
このようなときに、直角三角形になるような円周角をとります。すると、簡単に$\cos \beta$の値が求められます。
回答
$\angle XZW=90°$となるような点$W$をとります。
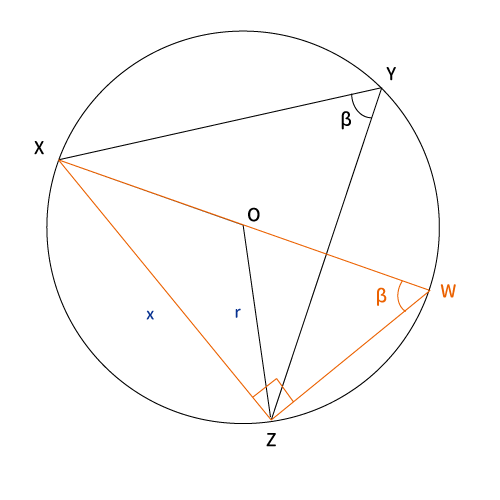
そうすると、$\bigtriangleup XZW$ は直角三角形です。
「円周角の定理」より
「円周角の定理」より$\angle XWZ=\beta$、更に直角三角形の場合、斜辺は外接円の直径になるので$XW=2r$が分かります。
三平方の定理より
三平方の定理より、$XW^2=XZ^2 + ZW^2$なので、$(2r)^2=x^2+ZW^2$となります。
つまり、$ZW$の長さが分かります。
よって、$\bigtriangleup XZW$は直角三角形なので、$\displaystyle \cos \beta = \frac{2r}{ZW}$と分かりました。
※$\sin \beta$も求められますね
まとめ
「1つの円弧に対する円周角はどの円周角も等しくなる」という性質はとても使い勝手が良いのでぜひ覚えておきたいです。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
円周角の定理、円弧、三平方の定理





