
事象$A$と$B$が独立しているとき、$P(A) \cap P(B)=P(A) \times P(B)$となることを確認したいと思います。
記号の説明
$P(A)$・・・事象$A$が起こる確率
$P(B)$・・・事象$B$が起こる確率
$P(A) \cap P(B)$・・・事象$A$と$B$がどちらも起こる確率
事象$A$と$B$が独立しているとは
事象$A$と$B$が独立しているとは、$A$と$B$はお互いに影響を受けないという意味です。
たとえば、コインを$1$回投げて「表」が出る確率を$P(A)$、サイコロを$1$回振って$1$が出る確率を$P(B)$とします。
このとき、$A$と$B$はお互いの確率に影響を与えるでしょうか?
コインを$1$回投げて「表」が出たとき
コインを$1$回投げて「表」が出ました。このとき、サイコロを$1$回振って$1$が出るかどうかに影響を与えるでしょうか?
いいえ、影響はありません。当たり前ですが、コインが「表」だろうが「裏」だろうが、サイコロで$1$が出る確率は$\displaystyle \frac{1}{6}$です。
サイコロを$1$回振って$1$が出たとき
サイコロを$1$回振って$1$が出たときも同様です。サイコロが「$1$」~「$6$」のどれが出ていようが、コインを$1$回投げて「表」が出る確率は$\displaystyle \frac{1}{2}$です。
$P(A) \cap P(B)=P(A) \times P(B)$
事象$A$と$B$が独立しているとき、$P(A) \cap P(B)=P(A) \times P(B)$はどうして成り立つのでしょうか?
引き続き上の例で見ていきましょう。
事象$A$・・・コインを$1$回投げて「表」が出る
事象$B$・・・サイコロを$1$回振って$1$が出る
上で見たとおり、事象$A$と$B$は独立しています。
まず、それぞれの確率を見ていきます。
$P(A)$:コインを$1$回投げて「表」が出る確率
全体が「表が出る、裏がでる」の2つ。確率を調べたいのは「表が出る」の1つ。
表が出る確率は、全体2つ起こるうちの1つが起こる割合なので、$\displaystyle \frac{1}{2}$となります。
$P(B)$:サイコロを$1$回振って$1$が出る確率
全体が「1の目が出る、2の目が出る、…、6の目が出る」の6つ。確率を調べたいのは「1の目が出る」の1つ。
1の目が出る確率は、全体6つ起こるうちの1つが起こる割合なので、$\displaystyle \frac{1}{6}$となります。
では、$P(A) \cap P(B)$:コインを$1$回投げて「表」が出る、かつ、サイコロを$1$回振って$1$が出る確率はどうなるでしょう。
$P(A) \cap P(B)$:コインを$1$回投げて「表」が出る、かつ、サイコロを$1$回振って$1$が出る確率
全体(分母)
全体つまり分母は下記の通り、12通りです。

計算方法は簡単です。3つの箱にリンゴが2個ずつ入っていたら全部で何個ですか?$3 \times 2=6$個ですよね。これと全く同じです。
コインの方の全体である「表が出る、裏がでる」の2パターンに対して、サイコロの方の全体である「1の目が出る、2の目が出る、…、6の目が出る」の6パターンを掛けるだけです。$2 \times 6 = 12$
確率を求めたい事象(分子)
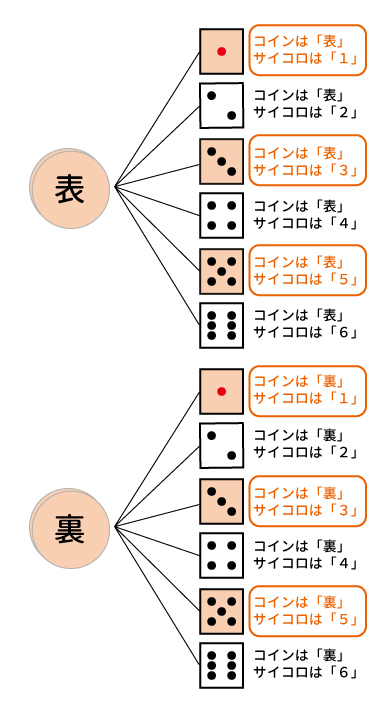
『コインを$1$回投げて「表」が出る、かつ、サイコロを$1$回振って$1$が出る』なので、下図の薄いオレンジに塗り潰した1通りです。

こちらの計算方法も同様で、3つの箱にリンゴが2個ずつ入っていたときの計算と同じです。
コインの方の「表が出る」1パターンに対して、サイコロの方の「1の目が出る」の1パターンを掛けるだけです。$1 \times 1 = 1$
この問題の場合1通りになるので、もう1パターン見ておきます。
上記は『コインを$1$回投げて「表」が出る、かつ、サイコロを$1$回振って$1$が出る』なので、『コインを$1$回投げて「表」か「裏」が出る、かつ、サイコロを$1$回振って奇数が出る』を考えてみましょう。
下図より分かるように6通りです。
こちらの計算方法も同様で、3つの箱にリンゴが2個ずつ入っていたときの計算と同じです。
コインの方の「表が出る」「裏が出る」2パターンに対して、サイコロの方の「奇数が出る」の3パターンを掛けるだけです。$2 \times 3 =6$。数えた6通りと同じ結果になりました。
$P(A) \cap P(B)$
上記より、$P(A) \cap P(B)$の分母が12、分子が1と分かりました。
よって、$\displaystyle P(A) \cap P(B) = \frac{1}{12}$
$P(A) \cap P(B)=P(A) \times P(B)$
$P(A) \cap P(B)=P(A) \times P(B)$、こちらの公式でも計算してみましょう。
同じ確率が算出されました。
理由
上記「全体(分母)」「確率を求めたい事象(分子)」を求めたのが理由そのものになります。
分母は、コインの方の全体である「表が出る、裏がでる」の2パターンに対して、サイコロの方の全体である「1の目が出る、2の目が出る、…、6の目が出る」の6パターンを掛ける、つまり$2 \times 6 = 12$です。
分子は、コインの方の「表が出る」1パターンに対して、サイコロの方の「1の目が出る」の1パターンを掛ける、つまり$1 \times 1 = 1$です。
分母・分子ともに各確率の分子と分母をそれぞれ掛けたものです。これはまさに$P(A) \times P(B)$ですね。
では最後に、影響を受ける場合も参考までに考えてみましょう。
(参考)事象$A$と$B$がお互いに影響を受ける
事象$A$と$B$がお互いに影響を受ける例を見て、イメージを掴んでみましょう。
サイコロを1回振って、1が出る確率を$P(A)$、奇数が出る確率を$P(B)$とします。
1が出る確率$\displaystyle P(A)=\frac{1}{6}$です。奇数が出る確率$\displaystyle P(B)=\frac{3}{6}=\frac{1}{2}$です。
では、サイコロを1回振って、「1が出る」かつ「奇数が出る」確率$P(A \cap B)$はどうなるでしょう?
$P(A \cap B)=P(A) \times P(B)$が成り立つと仮定
$P(A \cap B)=P(A) \times P(B)$が成り立つと仮定して計算してみます。
$\displaystyle P(A) \times P(B) = \frac{1}{6} \times \frac{1}{2} = \frac{1}{12}$
さて、サイコロを1回振って、「1が出る」かつ「奇数が出る」確率$P(A \cap B)$は$\displaystyle \frac{1}{12}$でしょうか?
いいえ、違います。答えは$\displaystyle \frac{1}{6}$です。
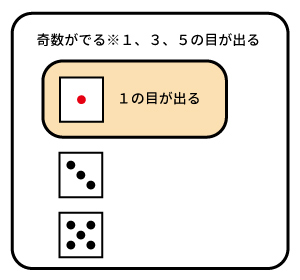
よく考えてみると当たり前ですね。「1が出る」かつ「奇数が出る」確率とは、単に「1が出る」確率のことです。
下記のように「1が出る」が「奇数が出る」に含まれるから$A \cap B=A$となるわけですね。
影響を受けるとは
1が出る確率を$P(A)$は$\displaystyle \frac{1}{6}$です。では、「奇数が出た」ときも「1である」確率は$\displaystyle \frac{1}{6}$でしょうか?
「奇数が出た」わけなので出た目は「1」「3」「5」のいずれかになります。つまり、「1」「3」「5」の中で「1」である確率なので$\displaystyle \frac{1}{3}$になります。これは、1が出る確率を$P(A)$は$\displaystyle \frac{1}{6}$とは異なります。
このようにどちらかの事象が起きたとき、もう一方の確率に影響を与える場合があります。
こういった場合には、$P(A \cap B)=P(A) \times P(B)$が成り立ちません。よって「$A$と$B$が独立しているとき」という条件が付くのですね。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
確率、事象の独立、$P(A \cap B)=P(A) \times P(B)$





