例えば、$\bigtriangleup ABC$の$\angle ACB$の二等分線と$AB$との交点を$D$とします。
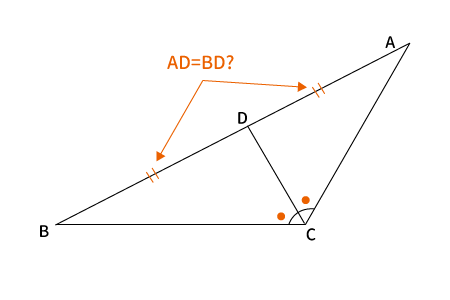
まず、$\angle ACB$の二等分線なので、$\angle ACD = \angle BCD$が成り立つことはすぐに分かります。
では、$AB$も二等分されて、$AD=BD$となるのでしょうか?
結論
結論から言うと、「線分の二等分線」は線分を二等分にしますが、「角の二等分線」は角は二等分しますが、線分は二等分するとは限りません。
線分の二等分線
線分の二等分線を知っていますか?
文字のとおり、線分を二等分する線です。下記のように$AB$を二等分している線のことです。二等分しているので$AC=BC$となります。ちなみに$C$は$AB$の中点です。

線分を二等分にすればよいので、下記のような線も二等分線となります。
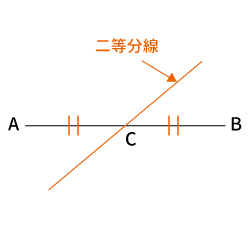
線分の二等分線は$AB$と平行にさえならなければ、どのような角度で$AB$と交わっても大丈夫ということですね。つまり、「線分の二等分線」は1つだけではなくいくつも存在することが分かります。
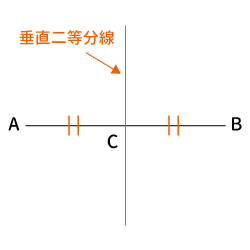
また、下記のように線分と垂直に交わる二等分線を垂直二等分線と言います。こちらの方が聞き馴染みがあります。
角の二等分線
角の二等分線を知っていますか?
文字のとおり、角を二等分する線です。下記のように$\angle ABC$を二等分している線のことです。二等分しているので$\angle \color{orange}●$は同じ角度になります。
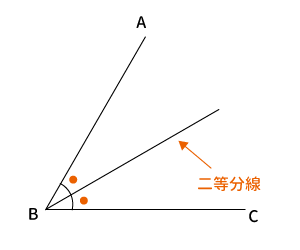
「角の二等分線」は「線分の二等分線」とは違い、一つの角に対して1つしかありません。
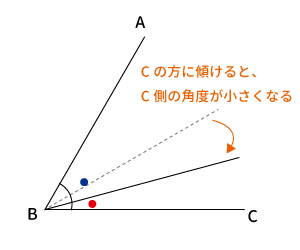
1つしかない理由
もし、点$C$の方にずらせば、下図のように$\angle \color{red}● $より $\angle \color{blue}●$の方が大きくなるため、角を二等分できていないので、二等分線ではありません。
下図も同様で点$A$の方にずらせば、$\angle \color{blue}● $より $\angle \color{red}●$が大きくなるため、角を二等分できていないので、二等分線ではありません
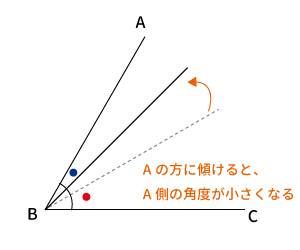
よって、角の二等分線はどちらの方向にもずらせないので、1本しかありません。
「角の二等分線」って辺も二等分するの?
ようやく本題です。
「角の二等分線」って辺も二等分するの?とはどういうことか上の「角の二等分線」の図を例に説明します。

上図の「角の二等分線」と$AC$の交点を$D$とするとき、$AD=CD$になるのか?ということです。
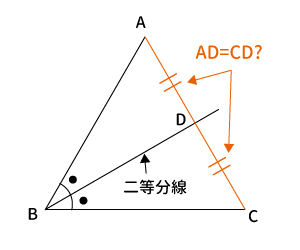
一番簡単な方法は反例を見つけることです。
$30^{\circ}$、$60^{\circ}$の直角三角形が計算しやすいので、そちらで確認してみましょう。
$30^{\circ}$、$60^{\circ}$の直角三角形の場合
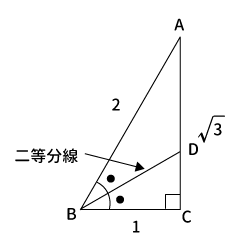
下記内容で正しく作図してみました。
- $\angle ABC = 60^{\circ}$
- $\angle BAC = 30^{\circ}$
- $\bigtriangleup ABC$は直角三角形
- $AB=2$、$BC=1$、$AC=\sqrt{3}$
- $\angle ABC$の二等分線と$AC$が交わる点を$D$とする
図を見てわかる通り$AD \neq AC$ですね。
よって、「角の二等分線」は角は二等分にするが、線分を二等分にするわけではないということが分かりました。
(参考)$AD$、$CD$を計算する
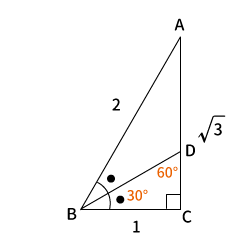
$BD$は$\angle ABC$を二等分しているので、$\angle CBD=60^{\circ}\div 2=30^{\circ}$
三角形の内角の和は$180^{\circ}$なので、$\angle BDC=180^{\circ}-30^{\circ}-90^{\circ}=60^{\circ}$
よって、$\bigtriangleup BCD$も$30^{\circ}$、$60^{\circ}$の直角三角形ということが分かりました。つまり、$CD:BD:BC=1:2:\sqrt{3}$となります。
従って、$CD:BC=1:\sqrt{3}$です。
$CD:BC=1:\sqrt{3}$
$\sqrt{3}CD=BC$
$BC=1$なので、
$\sqrt{3}CD=1$
$\displaystyle CD=\frac{1}{\sqrt{3}}$
$\displaystyle CD=\frac{\sqrt{3}}{3}$
$CD$は$\displaystyle \frac{\sqrt{3}}{3}$となります。
$\displaystyle AD=\sqrt{3}-\frac{\sqrt{3}}{3}$なので、$\displaystyle AD=\frac{2\sqrt{3}}{3}$です。
点$D$は$AC$を$2:1$するようです。
(参考)正三角形であれば、角の二等分線で線分も二等分される
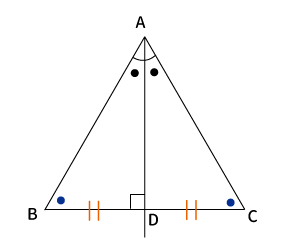
正三角形の場合をざっと説明します。
正三角形の場合、すべての内角が$60^{\circ}$です。また$AD$は二等分線なので、 $\angle BAD = \angle CAD = 30^{\circ}$となります。
つまり、$\bigtriangleup ABD$と$\bigtriangleup ACD$は3角とも同じなので、合同です。
よって、$BD=CD$となります。
このように線分も二等分される場合もあります。
まとめ
「角の二等分線」が線分までも二等分してしまうと思い込んで問題を解いていくと間違ってしまいます。
計算が合わずに途中で気づいたとしても、テストなどであればタイムロスが大きいです。
勘違いしないように注意したいですね。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
二等分線、線分の二等分線、角の二等分線、三角比