コインを3回投げて「表」が2回、「裏」が1回出るのは3通りというのは数えれば簡単です。
ですが、これ$_3C_1$で求められるんです。例題のように3回投げた場合であれば、数えてもすぐ分かります。ですが、10回、100回と試行回数が増えるとどうでしょう?大変ですよね。
数えてみる
まずは、コインを3回投げて「表」が2回、「裏」が1回出る場合を数えてみましょう。
| No | 1回目 | 2回目 | 3回目 |
|---|---|---|---|
| パターン$1$ | 表 | 表 | 裏 |
| パターン$2$ | 表 | 裏 | 表 |
| パターン$3$ | 裏 | 表 | 表 |
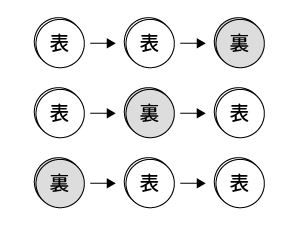
上の表、画像からも分かるとおり、数えると3通りでした。
$_3C_1$で求められる?
では、本題です。
『コインを3回投げて「表」が2回、「裏」が1回出る』がなぜ$_3C_1$で求められるのでしょうか。
$_3C_1$とは?
$_3C_1$とは、組み合わせと言って、$_3C_1$の場合だと、「3個のものから1個取った組み合わせ」の総数になります。
組み合わせ自体については深く触れませんが、2つほど例を見ておきます。
例1:3人の学生から1人を選ぶ組み合わせは何通り?
3人の学生がAさん、Bさん、Cさんとします。この3人の学生から1人を選ぶ組み合わせは「Aさん」「Bさん」「Cさん」の3通りです。数えるまでもないですね。
「3人の中から1人を選ぶ組み合わせ」なので組み合わせの公式を使うと$_3C_1$となります。
これを計算すると、$\displaystyle _3C_1=\frac{3}{1}=3$通りなので合っていますね。
例2:5種類の果物の中から3種類 選ぶ組み合わせは何通り?
果物は「リンゴ」「ミカン」「バナナ」「ブドウ」「モモ」の5種類あります。
この5種類の果物の中から3種類 選びます。今回は先に組み合わせの公式を使います。「5種類から3種類選ぶ組み合わせ」なので$_5C_3$です。
これを計算すると、$\displaystyle _5C_3=\frac{5・4・3}{3・2・1}=10$通りです。
たとえば、「リンゴ」「ミカン」「バナナ」の場合、順番を考慮しなければならない場合は、「リンゴ」「ミカン」「バナナ」、「リンゴ」「バナナ」「ミカン」、「ミカン」「リンゴ」「バナナ」・・・というように合計6通りとなります。※順番が絡む場合は階乗といい、$3!=3・2=6$通りになります
「組み合わせ」の場合は選んだ順番などは関係ないので、「リンゴ」「ミカン」「バナナ」と「リンゴ」「バナナ」「ミカン」を分けて考える必要はありません。どちらも「リンゴ」と「ミカン」と「バナナ」が選ばれているという点ではどれから選んだとしても同じです。
$\displaystyle _5C_3$はこの順番を入れ替えてできるパターンを除外してくれているのです。
下記の通り、数えても10通りでした。
| No | 1種類目 | 2種類目 | 3種類目 |
|---|---|---|---|
| パターン$1$ | リンゴ |
ミカン |
バナナ |
| パターン$2$ | リンゴ |
ミカン |
ブドウ |
| パターン$3$ | リンゴ |
ミカン |
モモ |
| パターン$4$ | リンゴ |
バナナ |
ブドウ |
| パターン$5$ | リンゴ |
バナナ |
モモ |
| パターン$6$ | リンゴ |
ブドウ |
モモ |
| パターン$7$ | ミカン |
バナナ |
ブドウ |
| パターン$8$ | ミカン |
バナナ |
モモ |
| パターン$9$ | ミカン |
ブドウ |
モモ |
| パターン$10$ | バナナ |
ブドウ |
モモ |
『コインを3回投げて「表」2回「裏」1回出るのは何通り?』が$_3C_1$で求められる理由
コインを3回投げて「表」2回「裏」1回出るのは何通り?
最初にも触れましたが、答えは下記のとおり3通りです。

この問題を下記のように捉えると$_3C_1$が使えるようになります。
問題を読み替える1
コインを3回投げて「表」2回「裏」1回出るのは何通り?は、下記のように捉えることができます。
3つの空欄から(「裏」を記入するための)1つの空欄を選ぶ組み合わせは何通り?
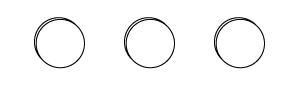
これは3つの内から1つを選ぶ組み合わせなので、$\displaystyle _3C_1=\frac{3}{1}=3$通りで、数えると下記のとおりです。

さて、この上の画像ですが、空白を「表」と捉えて矢印を追加すれば、「コインを3回投げて「表」2回「裏」1回出るのは何通り?」と全く同じですよね。
言い換えただけなので、結果が同じになるのは当然なのですが、比較すると分かりやすいですね。
上では「3つの空欄から(「裏」を記入するための)1つの空欄を選ぶ」としましたが、「3つの空欄から(「表」を記入するための)2つの空欄を選ぶ」と読み替えても大丈夫です。
問題を読み替える2
コインを3回投げて「表」2回「裏」1回出るのは何通り?は、下記のようにも捉えることができます。
3つの空欄から(「表」を記入するための)2つの空欄を選ぶ組み合わせは何通り?

これは3つの内から2つを選ぶ組み合わせなので、$\displaystyle _3C_2=\frac{3・2}{2・1}=3$通りで、数えると下記のとおりです。
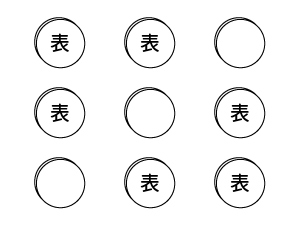
さて、この上の画像ですが、空白を「裏」と捉えて矢印を追加すれば、「コインを3回投げて「表」2回「裏」1回出るのは何通り?」と全く同じですよね。
「3つの空欄から(「裏」を記入するための)1つの空欄を選ぶ組み合わせは何通り?」と読み替えたときと同じ結果ですね。
まとめ
コインを3回投げて「表」2回「裏」1回出るのは何通り?
だけ見ると「組み合わせ」とはあまり思えませんが、この問題がどういったものかを整理し、理解すると「組み合わせ」として捉えることができ簡単に何通りあるか計算することができるようになります。
組み合わせや確率の問題に関わらず、他の問題でも違う方向からの視点を持つことで様々な解決策を見つけられるかもしれませんね。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
組み合わせ、順列、階乗