1次方程式 y=ax+b の平行移動

1次方程式 $y=x$ の$x$軸方向に平行移動

まず、簡単な式$y=x$から考えます。この直線を$l$とします。

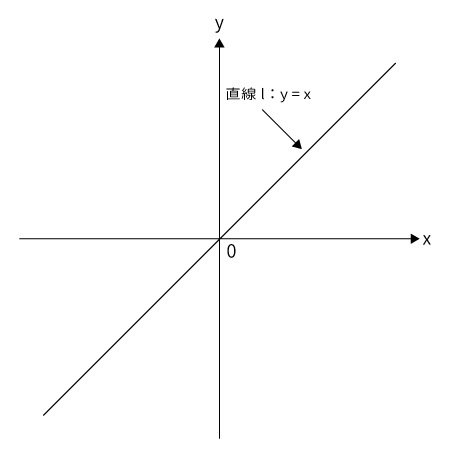
この一次方程式$y=x$を$x$軸方向に$d$だけ平行移動します。この直線を$m$とします。
※「distance（距離）」のdを使いました

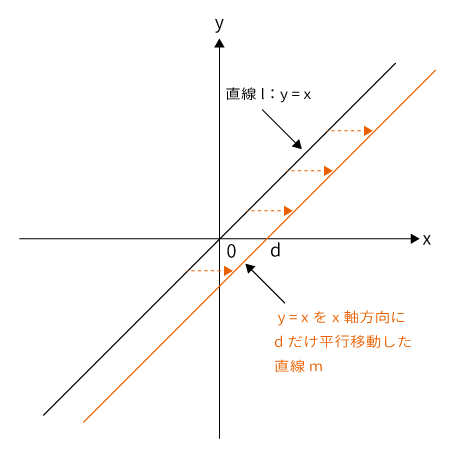
この平行移動した直線$m$はどのような式で表すことができるのでしょうか？

平行移動した直線の式

平行移動した「直線$m$が$x=d$のときの$y$の値」は「直線$l$が$x=0$のときの$y$の値」になります。

$x$が他の値のときも同様です。

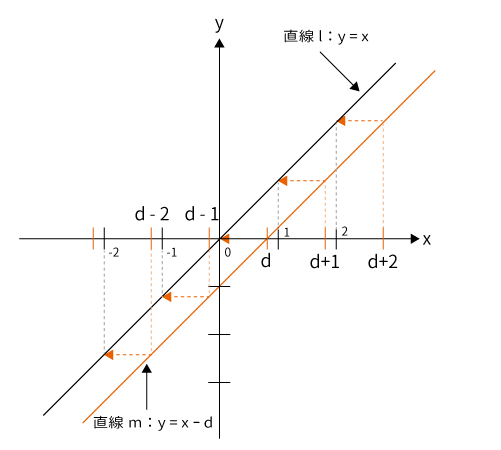
直線$m$	直線$l$
$x=d-2$	$x=-2$
$x=d-1$	$x=-1$
$x=d$	$x=0$
$x=d+1$	$x=1$
$x=d+2$	$x=2$

つまり、直線$m$はどのような$x$の値がきても$x$から$d$を引いて、直線$l$：$y=x$に渡せば、直線$m$の$y$の値が求められます。

よって、直線$l$：$y=x$の$x$を$x-d$に置き換えた式$y=x-d$が直線$m$の式となります。

1次方程式 $y=x$ の$y$軸方向に平行移動

$x$軸方向に平行移動するよりシンプルです。平行移動する前の$y=x$を直線$l$、平行移動した後の直線を$m$とします。

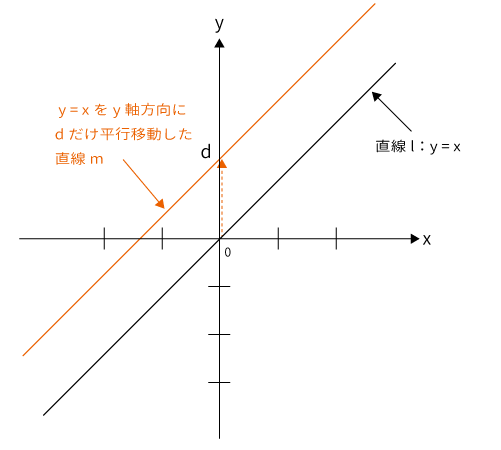
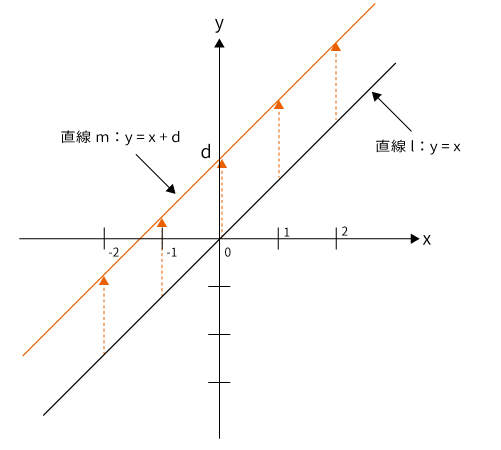
直線$m$は直線$l$：$y=x$を$y$軸方向に$d$だけ平行移動した直線です。

$x=0$のときを見てみましょう。$x=0$のとき直線$l$は$y=0$です。直線$m$は$y$軸方向に$d$だけ平行移動しているので、直線$l$の結果に$d$を足せばOKです。よって、直線$m$は$y=d$です。

$x$が他の値のときも同様です。

$x$	直線$l$の$y$	直線$m$の$y$
-2	-2	$-2+d$
-1	-1	$-1+d$
0	0	$d$
1	1	$1+d$
2	2	$2+d$

つまり、直線$m$はどのような$x$の値がきても$y=x$で算出された$y$の値に$d$を足すと直線$m$の$y$の値が求められます。

よって、直線$l$：$y=x$（$x$の関数）に$d$を加えた式$y=x+d$が直線$m$の式となります。

平行移動の公式

ここまでで、「平行移動すると式がどのように変化するか？」は、何となくイメージできたかと思います。

このようにグラフを平行移動したときの公式があります。

$y=x$を例に見てきたものと形が少し異なりますが、同じです。

$f(x)$というのは$x$の関数というもので、$y=x$も$x$の関数です。例に挙げた$y=x$は、$f(x)=x$ということです。

では、実際に先ほどの例で確認してみましょう。

先ほどの例で公式を試してみる

先ほどの例の結果をまとめておきます。

直線$l$：$y=x$を$x$軸方向に$d$だけ平行移動した直線$m$の式は$y=x-d$・・・( i )

直線$l$：$y=x$を$y$軸方向に$d$だけ平行移動した直線$m$の式は$y=x+d$・・・( ii )

$x$軸方向に平行移動した場合

$f(x)=x$、$y=f(x)$を$x$軸方向に$d$平行移動するので、$y=f(x-d)$

$f(x-d)$は$f(x)=x$の$x$に$x-d$を代入すればよいので、$y=f(x-d)=x-d$となります。

これは、 ( i ) と同じ結果でした。例も公式通りでした。

$x$軸方向に平行移動した場合

$f(x)=x$、$y=f(x)$を$y$軸方向に$d$平行移動するので、$y-d=f(x)$

よって、$y=f(x)+d$

$f(x)=x$なので、$y=f(x)+d=x+d$となります。

これは、 ( ii ) と同じ結果でした。例も公式通りでした。

まとめ

例を見ながら1次方程式が平行移動したらどのように式が変化するか見てみました。

今後、実際に公式の証明が出来ればと思います。

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

1次方程式、平行移動、グラフ、グラフの平行移動の公式、直線