
$0.999…=1$
僕が中学生の頃、ある先生が授業の始めに話してくれたことを今でも覚えています。
証明はとても簡単で、たまーに思い出してはどんな証明だったかなと考えたりします。
0.999…=1の証明
無限小数$0.999…$を$x$と置きます。
$x=0.999…$・・・( i )
( i ) $x=0.999…$の(両辺)に$10$を掛けます。
$10x = 9.999…$・・・( ii )
( ii ) – ( i )
( ii ) – ( i ) をすると、
(左辺)$=10x-x = 9x$・・・( iii )
ここは特に気になる点はないと思います。
(右辺)$=\color{red} 9.999…-0.999…=9$・・・( iv )
ここが今回の肝になります。
すんなり受け入れれる人と、そうではない人がいると思います。後ほど受け入れにくい理由を説明します。
証明はすぐに終わるので先に終わらせておきますね。
では、上の( iv ) (右辺)$=9.999…-0.999…=9$が成り立つとして進めます。
( iii )が左辺 で ( iv )が右辺なので、( iii ) = ( iv )となり、
$9x = 9$
ゆえに、$x=1$となります。
( i ) より、$x=0.999…$なので、$0.999…=1$となります。
以上で、証明は終了です。
では、問題の(右辺)$=9.999…-0.999…=9$・・・( iv )について少し掘り下げて考えてみましょう。
$9.999…-0.999…=9$について
引っかかる点は「$9.999…$」と「$0. 999…$」の小数点以下の”$9$”の個数ではありませんか?
その理由は下記のように感じる場合があるからだと思います。

$0.999…$に$10$を掛けると、「$9. 999…$」と桁が繰り上がるので、小数点以下の$9$の個数が1つ減ったように感じます。
もし実際に減ったとすれば、「$9.999…$」と「$0.999…$」の小数点以下の$9$の個数は1つ違うはずです。そうであれば、$9.999…-0.999…$の小数点以下がきれいに消えるのはおかしいよね?ということです。
桁が変わると感じるのには、理由があります。
それは、無限小数ではない場合を知っているからです。
では、$x=0.999$の場合を考えてみましょう。こちらを同じように両辺10倍してみます。
$10x=9.99$となります。同様に、$10x=9.99$と$x=0.999$の各辺を引きます。
(左辺)$=10x-x=9x$で同じですね。
(右辺)$=9.99-0.999=8.991$…小数点以下が全く消えていないですね。小数点以下の$9$の数が2個と3個で違うためです。
さて、このような結果になることは、ほとんどの方が知っていますし、理解できます。
そして、無限小数$0.999…$の場合もこれと同じ現象が起きると考えるのです。
無限小数の小数点以下はやっぱり無限
下図のとおり、無限小数は10倍してもやはり無限小数です。「$9.999…$」と「$0.999…$」の小数点以下の$9$の個数はどちらも無限です。

少し具体的にみてみます。
その前に、無限についてのお話があるので、ご紹介します。
無限についてのお話
「数学はいつも苦手だった」という本があるのですが、その中に無限について悪魔とカラスが会話しているお話があります。
関連がある箇所だけをかいつまんでお話しすると、
無限人の学生が無限個の席に座っています。1つの座席には1人ずつ座っています。
ここで遅れて1人学生がやってきました。このとき、遅れてきた学生も含め学生は全員席に座れるのでしょうか?
どう思いますか?
まず、遅れてきた人は最初の席に座っている学生に席を譲ってもらいます。遅れてきた学生は席に座れましたが、1つ目の席に座っていた学生は立っている状態になってしまいました。
次に、1つ目の席に座っていた学生は2つ目の席に座っている学生に席を譲ってもらいます。今度は1つ目の席に座っていた学生は席に座れましたが、2つ目の席に座っていた学生は立っている状態になってしまいました。
これを繰り返していきます。ここの学生さんはみんな優しいですね。
では、もう少し見てみましょう。
今、10,000番目の席に座っていた学生が立っている状態です。ですが、同じように10,001番目の席に座っている学生に席を譲ってもらいます。10,000番目の席に座っていた学生も無事座ることが出来ました。
さらに飛んで1兆番目の席に座っていた学生が立っている状態です。この学生も同様1兆1番目の席に座っている学生に席を譲ってもらいました。1兆番目の席に座っていた学生もまた無事座れました。
さて、何番目の学生が座れなくなるのでしょうか?
そうです。何番目であろうと、次の席の学生に席を譲ってもらうことができるのです。つまり、席に座れない学生はいないのです。
これが無限というモノです。
$9.999…-0.999…$も同じ
上の座席の話と同じように考えると、$9.999…-0.999…$も小数点以下がきれいに消えることが分かります。
まず、ずれていることが分かるように$0.999$の時点で小数点以下の$9$に番号を振っておきましょう。
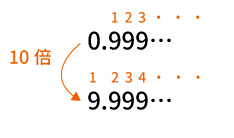
「$9.999…$の小数点以下最初の$9$、つまり$2$番の$9$」は「$0.999…$の$1$番の$9$」によって消せます。※番号は上図に従っています
次に、「$9.999…$の$3$番の$9$」は「$0.999…$の$2$番の$9$」によって消せます。
では、「$9.999…$の$5,692$番の$9$」はどうでしょう?
そうです。「$0.999…$の$5,691$番の$9$」によって消せます。
つまり、上の座席の話と同じで、「$9.999…$の$n$番目の$9$」は「$0.999…$の$n-1$番目の$9$」によって消せます。つまり、何番目の$9$も消せるので、すべて消すことができます。
よって、$9.999…-0.999…$の小数点以下の$.999…$はすべて消えて$9.999…-0.999…=9$となります。
このように、無限小数であれば、このような結果になるわけです。
証明は先に終えていますので、以上となります。
まとめ
無限についてあまり知らないときに、この証明を見せられるとマジックを見せられたような気持ちになります。
僕はこの話を聞く前から数学は割と好きでしたが、こんな感じで普通の授業からは少し脱線する話をしてくれると、数学を好きになる人も増えそうな気がします。
数学以外でも自分の好奇心を刺激してくれるような先生がいると良いですね。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
無限、無限小数、極限、循環小数





