$\sin \theta$、$\cos \theta$、$\tan \theta$と$\sin(180^{\circ}-\theta)$、$\cos(180^{\circ}-\theta)$、$\tan(180^{\circ}-\theta)$の値の関係性を知っているとテストなどでも役に立ちます。
単位円を用いて、どのような関係性があるのか調べたいと思います。
単位円について気になる方は下記をご覧ください。
単位円とは原点を中心とする半径1の円のことです。 この単位円を使うことで、$sin$、$cos$の値を簡単な形で表すことができます。三角比を考える上で非常に便利なツールなので覚えておくことをオススメします。 単位円 …
結論
$\cos(180^{\circ}-\theta)=-\cos\theta$
$sin(180^{\circ}-\theta)=sin\theta$
$\displaystyle \tan(180^{\circ}-\theta)=-\tan \theta$
$180^{\circ}-\theta$とは
$180^{\circ}$と$\theta$を図示して$180^{\circ}-\theta$がどのようなものか確認してみましょう。
$\theta < 180^{\circ}$の場合
$\theta < 180^{\circ}$の場合、$180^{\circ}$と$\theta$を図示すると下図のようになります。

よって、$180^{\circ}-\theta$は$180^{\circ}$から$\theta$を除いた部分(下図青部)なので下のようになります。

単位円に合わせるために、$180^{\circ}-\theta$を水平方向に反転させておきます。
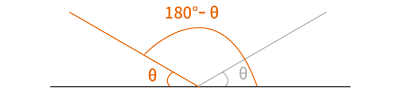
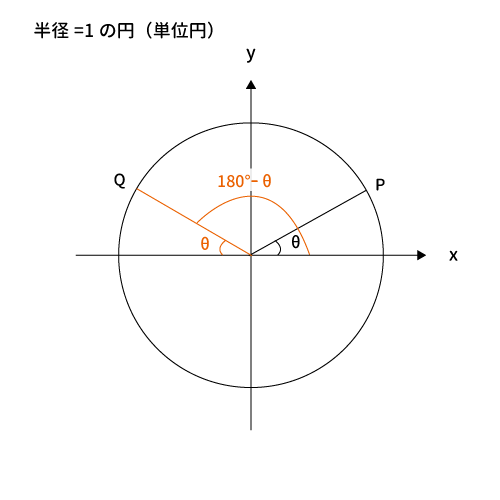
単位円で見ると下記のようになります。詳しくは後ほど確認しますが、点$P$と点$Q$は$Y$軸を基準に反転した座標です。つまり、$X$軸はプラスマイナスが反対で、$Y$座標は同じになります。$P$、$Q$は同じような値で座標を表せそうですね。
$180^{\circ} < \theta < 360^{\circ}$の場合
$180^{\circ} < \theta < 360^{\circ}$の場合、$180^{\circ}$と$\theta$を図示すると下図のようになります。

$180^{\circ} < \theta$なので、$180^{\circ}-\theta$はマイナスになるので絶対値にして図示しました。
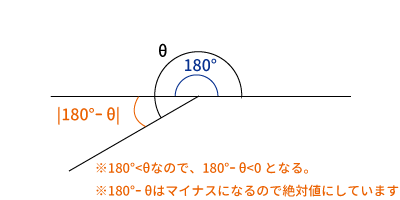
時計回りがプラス方向、反時計回りがマイナス方向になります。

単位円に合わせるために、$180^{\circ}-\theta$を水平方向に反転させておきます。
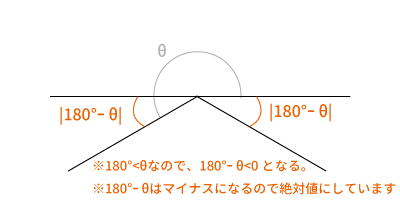
単位円で見ると下記のようになります。詳しくは後ほど確認しますが、点$P$と点$Q$は$Y$軸を基準に反転した座標です。$\theta < 180^{\circ}$の場合と同じく$P$、$Q$は同じような値で座標を表せそうです。

単位円を用いて$\sin(180^{\circ}-\theta)$、$\cos(180^{\circ}-\theta)$、$tan(180^{\circ}-\theta)$がどうなるか確認する
単位円は、原点$O$、点$S(1, \, 0)$、円周上の点$P$に対して$\angle POS=\theta$とすると、$P$の座標を$(\cos \theta, \, \sin \theta)$、つまり$x=\cos \theta$、$y=\sin \theta$と定義しています。また、$tan \theta$は$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$と定義されています。
角度は$OS$を基準に何度か決まるわけですね。
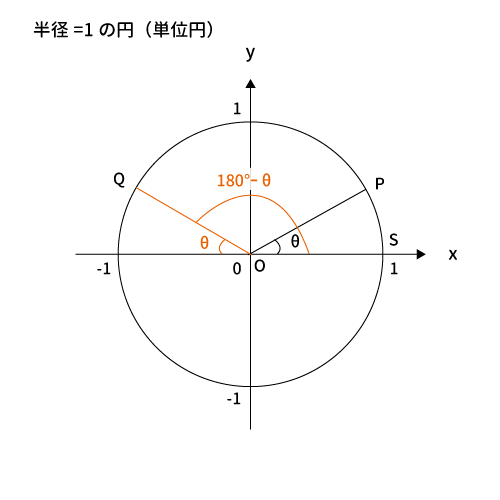
$0^{\circ} < \theta < 180^{\circ}$の場合

上図のとおり、$\theta$、$180^{\circ}-\theta$の各座標は下記のとおりです。
$\theta$の座標は$(\cos\theta, \, sin\theta)$
$180^{\circ}-\theta$の座標は$(\cos(180^{\circ}-\theta), \, sin(180^{\circ}-\theta))$
ここで、下図の赤と青の三角形を見てください。
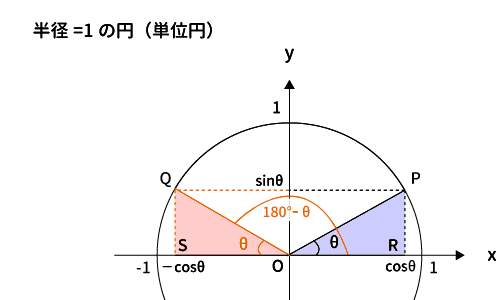
この2つの三角形はともに直角三角形です。そして、原点と接する角$\angle QOS$、$\angle POR$はともに$\theta$です。従って残り一つの角も同じになります。
また、斜辺$OQ$、$OP$はともに単位円の半径なので$1$です。
合同
上記より下記を満たすので$\bigtriangleup OQS \equiv \bigtriangleup OPR$(合同)です。
- $OQ=OP$
- $\angle QOS = \angle POR$
- $\angle OQS = \angle OPR$
- 上3つより、1組の辺とその両端の角がそれぞれ等しい
$\bigtriangleup OQS \equiv \bigtriangleup OPR$(合同)より

$\bigtriangleup OQS \equiv \bigtriangleup OPR$(合同)より、角辺がそれぞれ等しい。
つまり、点$P$と点$Q$の座標の数値が等しいということです。ただし、点$Q$はX軸のマイナス側にあるので、点$P$の$x$座標をマイナスにした値となります。
点$P$の座標は$(\cos\theta, \, sin\theta)$なので、点$Q$の座標は$(-\cos\theta, \, sin\theta)$と書くことができます。
各座標が等しいので、$\cos$と$\sin$の関係性は下記だと分かりました。
$\cos(180^{\circ}-\theta)=-\cos\theta$
$sin(180^{\circ}-\theta)=sin\theta$
$\cos$と$\sin$が分かったので、$\tan$も分かります。
$\displaystyle \tan(180^{\circ}-\theta)=-\tan \theta$
※単位円について気になる方は下記をご覧ください
単位円とは原点を中心とする半径1の円のことです。 この単位円を使うことで、$sin$、$cos$の値を簡単な形で表すことができます。三角比を考える上で非常に便利なツールなので覚えておくことをオススメします。 単位円 …
$180^{\circ} < \theta < 360^{\circ}$の場合
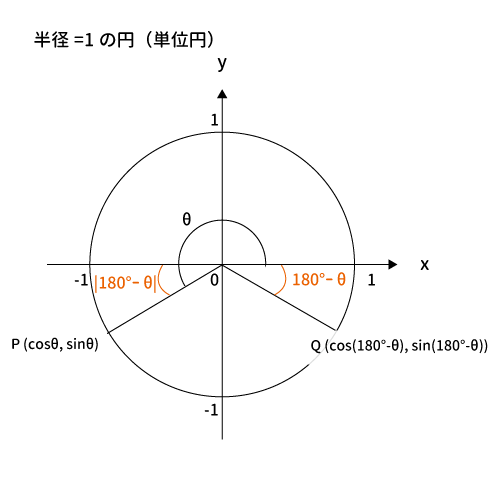
上図のとおり、$\theta$、$180^{\circ}-\theta$の各座標は下記のとおりです。
$\theta$の座標は$(\cos\theta, \, sin\theta)$
$180^{\circ}-\theta$の座標は$(\cos(180^{\circ}-\theta), \, sin(180^{\circ}-\theta))$
ここで、下図の赤と青の三角形を見てください。
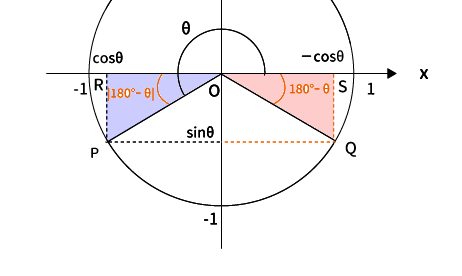
この2つの三角形はともに直角三角形です。そして、原点と接する角$\angle QOS$、$\angle POR$はともに$180^{\circ}-\theta$です。従って残り一つの角も同じになります。
また、斜辺$OQ$、$OP$はともに単位円の半径なので$1$です。
合同
上記より下記を満たすので$\bigtriangleup OQS \equiv \bigtriangleup OPR$(合同)です。
- $OQ=OP$
- $\angle QOS = \angle POR$
- $\angle OQS = \angle OPR$
- 上3つより、1組の辺とその両端の角がそれぞれ等しい
$\bigtriangleup OQS \equiv \bigtriangleup OPR$(合同)より

$\bigtriangleup OQS \equiv \bigtriangleup OPR$(合同)より、角辺がそれぞれ等しい。
つまり、点$P$と点$Q$の座標の数値が等しいということです。ただし、点$Q$はX軸のプラス側にあるので、点$P$がマイナス側にあるため$x$座標をマイナスにした値となります。
点$P$の座標は$(\cos\theta, \, sin\theta)$なので、点$Q$の座標は$(-\cos\theta, \, sin\theta)$と書くことができます。
各座標が等しいので、$\cos$と$\sin$の関係性は下記だと分かりました。
$\cos(180^{\circ}-\theta)=-\cos\theta$
$sin(180^{\circ}-\theta)=sin\theta$
$\cos$と$\sin$が分かったので、$\tan$も分かります。
$\displaystyle \tan(180^{\circ}-\theta)=-\tan \theta$
$180^{\circ} < \theta < 360^{\circ}$の場合も$0^{\circ} < \theta < 180^{\circ}$の場合と同じ結果になりました。
$0^{\circ}$、$180^{\circ}$のとき
$\theta=0^{\circ}$のとき、$180^{\circ}-\theta$は$180^{\circ}$であり、$\theta=180^{\circ}$のとき、$180^{\circ}-\theta$は$0^{\circ}$になります。
よって、それぞれの座標が分かればOKです。
$\theta=0^{\circ}$の座標は$(1, \, 0)$
$\theta=180^{\circ}$の座標は$(-1, \, 0)$
よって、$\cos 0^{\circ} = 1$、$\sin 0^{\circ} = 0$、$\cos 180^{\circ} = -1$、$\sin 180^{\circ}= 0$になります。
$\sin 0^{\circ} = \sin 180^{\circ} =0$なので、$\sin 0^{\circ}=\sin 180^{\circ}=\sin (180^{\circ}-0^{\circ})$
$\sin 180^{\circ}=\sin 0^{\circ}=\sin (180^{\circ}-180^{\circ})$
※$\tan$は$\sin$、$\cos$から計算するだけなので省略
$0^{\circ}$、$180^{\circ}$のときも成り立ちました。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
$180^{\circ}-\theta$、$sin \theta$、$cos \theta$、$tan \theta$、三角比




