方べきの定理？図を用いて分かりやすく証明

方べきの定理・・・記憶には全くありませんが、各定理の内容は知っていた気がします。

方べきの定理は対頂角や円周角の定理から簡単に示すことができます。

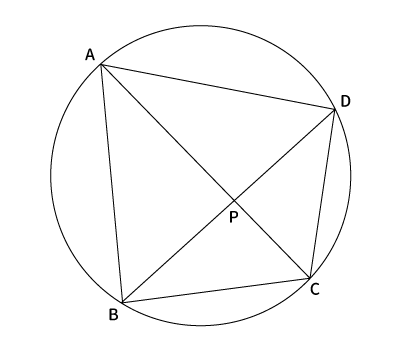
方べきの定理１：$PA・PC=PB・PD$

１つ目の方べきの定理は、円に内接する四角形$ABCD$の対角線の交点を$P$としたとき、$PA・PC=PB・PD$が成り立つ。これが１つ目の方べきの定理です。

証明

それでは証明してみます。

円周角の定理より$\angle BAC = \angle BDC$（※$\angle ●$）、$\angle APB$と$\angle CPD$は対頂角（向かい合う角）なので等しい（※$\angle ▲$）。

よって、$\bigtriangleup APB$と$\bigtriangleup DPC$は2組の角が等しいので、相似である。

対応する辺は$PA$と$PD$、$PB$と$PC$、$AB$と$DC$なので、$PA:PD=PB:PC$となり、$PA・PC=PB・PD$。

１つ目の方べきの定理が証明できました。

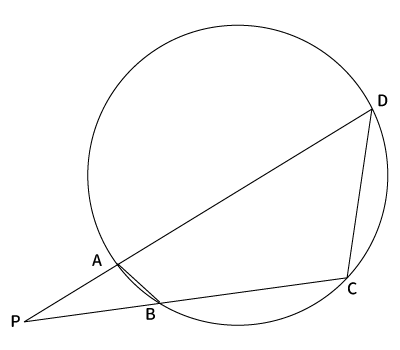
方べきの定理２：$PB・PC=PA・PD$

２つ目の方べきの定理は、円に内接する四角形$ABCD$の2辺の延長線上の交点を$P$としたとき、$PA・PD=PB・PC$が成り立つ。これが２つ目の方べきの定理です。

証明

それでは証明してみます。

円に内接する四角形の内角はその内角の対角の外角に等しいので、$\angle CDP = \angle ABP$（※$\angle ●$）。また、$\angle APB$と$\angle CPD$は共通の角なので等しい （※$\angle ▲$）。

よって、$\bigtriangleup ABP$と$\bigtriangleup CDP$は2組の角が等しいので、相似である。

 

対応する辺は$PA$と$PC$、$PB$と$PD$、$AB$と$CD$なので、$PA:PC=PB:PD$となり、$PA・PD=PB・PC$。

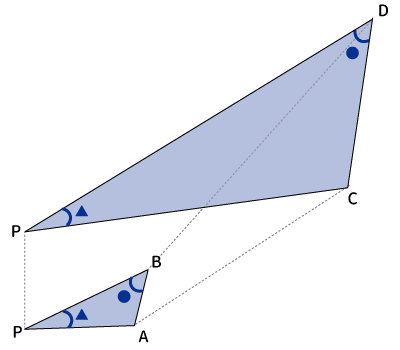
２つ目の方べきの定理が証明できました。

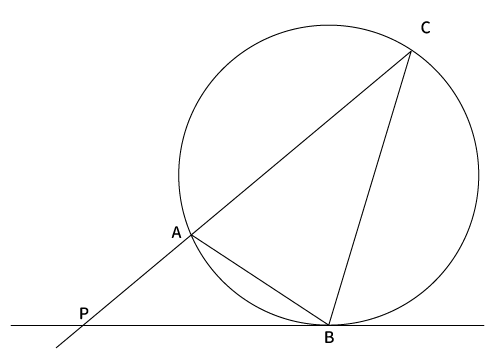
方べきの定理３：$PB・PC=PA・PD$

３つ目の方べきの定理は、円に内接する三角形$ABC$の直線$AC$と円に引いた$B$を接点とする接線の交点を$P$としたとき、$PA・PC=PB^2$が成り立つ。これが３つ目の方べきの定理です。

証明

それでは証明してみます。

上の定理１、２とは異なり、少し手間が掛かるので、先にざっくりとした流れを見てから、詳細にいきます。

ざっくりとした流れ

接線$PB$に対して接点$B$を通る垂線$DB$を引くと、円の中心を通る。すると、$\bigtriangleup ABD$は円に内接し、1辺が直径なので直角三角形となる。よって、下図のとおり、$\angle DBP$、$\angle DAB$が$90^{\circ}$となる。

あとは、円周角の定理から$\angle ADB$と$\angle ACB$が等しくなる（※$\angle ●$）ので、三角形の内角の和が$180^{\circ}$なので、いろいろと角度が分かって、$\bigtriangleup PAB$と$\bigtriangleup PBC$が相似だと分かり、$PA・PC=PB^2$が求まります。

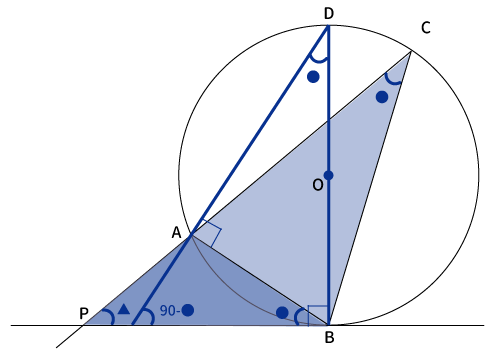
それでは、詳しく見ていきます。

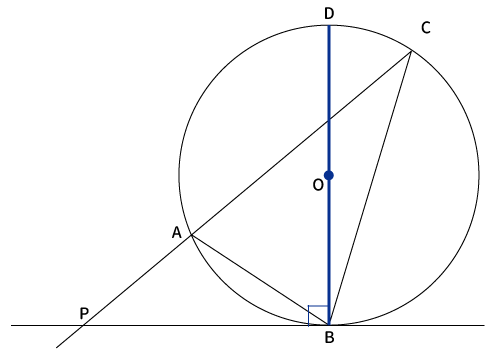
まず、直線$PB$に対して$B$を通る垂線を引き、円とのもう一方の交点を$D$とおく。

続いて、直線$DA$を引いて、接線$PB$との交点を$E$とおくと、円周角の定理より$\angle ADB= \angle ACB$。

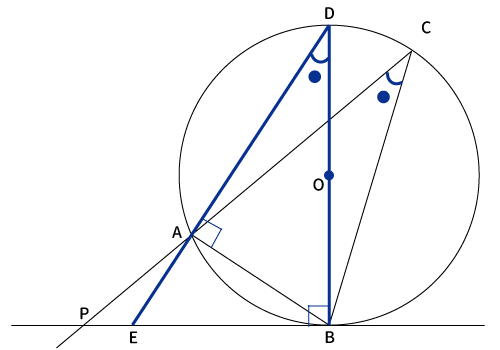
次に、三角形の内角の合計は$180^{\circ}$なので、$\angle BED=180^{\circ}-90^{\circ}-●=90^{\circ}-●$。

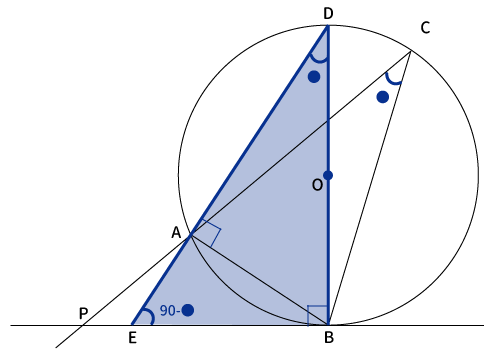
同様に、$\angle ABE=180^{\circ}-90^{\circ}-(90^{\circ}-●)=●$

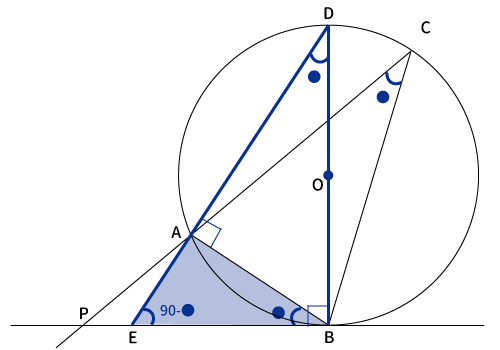
最後に$\angle APB$と$\angle BPC$は共通の角である。

よって、$\bigtriangleup ABP$と$\bigtriangleup BCP$は2組の角が等しいので、相似である。

対応する辺は$PA$と$PB$、$PB$と$PC$、$AB$と$BC$なので、$PA:PB=PB:PC$となり、$PA・PC=PB・PB=PB^2$。

３つ目の方べきの定理が証明できました。

以上、証明終了です。

まとめ

三角形と円が絡むと多くの角が関係を持ちます。問題が出されると、パズルみたいで上手く解ければ気持ちいいですが、沼にはまれば大変なことになりそうです…。

はまりそうであれば、次にいって時間が余っていれば戻ってくるのも良さそうですね。案外時間をあけると閃くこともあります。

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

方べきの定理、円周角の定理、対頂角、内接、外角、内角、相似