
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
問題
問題は下記を開いてご確認ください。
第3問 (1)
数列$\{a_n\}$は、初項$a_1$が$0$で、$n=1,\, 2,\, 3,\, ・・・$のとき次の漸化式を満たす。
(1)$a_2$の値は?
これは ( i ) に$n=1$を代入すればよい。
$a_1=0$なので、計算しつつ代入すると、
$\displaystyle a_{2}=2 (0 + 9-6)=6$
第3問(2)
※とにかく計算だらけですm(__)m
$\displaystyle b_n=\frac{a_n}{3^n(n+1)(n+2)}$とおく。
$\{b_n\}$の初項$b_1$は?
$\displaystyle b_n=\frac{a_n}{3^n(n+1)(n+2)}$に$n=1$を代入すればよい。
$\displaystyle b_1=\frac{a_1}{3^1(1+1)(1+2)}$
$a_1=0$、つまり分母が$0$なので$\displaystyle b_1=0$
$b_{n+1}$は?
$\displaystyle b_n=\frac{a_n}{3^n(n+1)(n+2)}$の$n$を$n+1$にすると、
$\displaystyle b_{n+1}=\frac{a_{n+1}}{3^{n+1}(n+2)(n+3)}$・・・( ii ) となる。
この式を変形していくと、左辺を( ii ) の右辺$\displaystyle \frac{a_{n+1}}{3^{n+1}(n+2)(n+3)}$の形にできそうである。
まず、両辺の分母に$(n+1)$があり消せる。また、右辺の分母の$(n+3)$が左辺に欲しいので移動すると、
あとは、両辺に$\displaystyle \frac{1}{3}$を掛ければよい
( ii )$\displaystyle b_{n+1}=\frac{a_{n+1}}{3^{n+1}(n+2)(n+3)}$より、
$\displaystyle b_{n+1}=\frac{3a_n + 3^{n+1}-(n+1)(n+2)}{3^{n+1}(n+1)(n+2)} $
続いてこの右辺を変形して、回答の形にしていく
$\displaystyle b_{n+1}=\frac{3a_n + 3^{n+1}-(n+1)(n+2)\}}{3^{n+1}(n+1)(n+2)} $
$\displaystyle \frac{a_n}{3^n(n+1)(n+2)}$は$b_n$なので、
$\displaystyle =b_n+\frac{1}{(n+1)(n+2)} -(\frac{1}{3})^{n+1} $
$\displaystyle b_{n+1}=b_n+\frac{1}{(n+1)(n+2)} -(\frac{1}{3})^{n+1} $・・・( iii )
$b_{n+1}-b_n$は?
( iii )$\displaystyle b_{n+1}=b_n+\frac{1}{(n+1)(n+2)} -(\frac{1}{3})^{n+1} $の$b_n$を左辺に移すと、
$\displaystyle b_{n+1}-b_n=\frac{1}{(n+1)(n+2)} -(\frac{1}{3})^{n+1} $
回答より、$\displaystyle \frac{1}{(n+1)(n+2)}=\frac{x}{n+1}-\frac{x}{n+2}$となれば良いので、(※$x=$キ)
$\displaystyle \frac{1}{(n+1)(n+2)}=\frac{x}{n+1}-\frac{x}{n+2}$
$\displaystyle \frac{1}{(n+1)(n+2)}=\frac{x(n+2)-x(n+1)}{(n+1)(n+2)}$
$\displaystyle 1=x(n+2)-x(n+1)$
$\displaystyle 1=nx+2x-nx-x$
$\displaystyle 1=x$
よって、$x$つまり「キ」は$1$なので、
$\displaystyle b_{n+1}-b_n = \frac{1}{n+1}-\frac{1}{n+2} -(\frac{1}{3})^{n+1} $・・・( iv )
$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{k+1}-\frac{1}{k+2})$は?
$n$は$2$以上の自然数とするので、
$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{k+1}-\frac{1}{k+2}) $
$\displaystyle =(\frac{1}{1+1}-\frac{1}{1+2})-(\frac{1}{2+1}-\frac{1}{2+2})-(\frac{1}{3+1}-\frac{1}{3+2})-・・・$
$\displaystyle ・・・-(\frac{1}{n-2+1}-\frac{1}{n-2+2})-(\frac{1}{n-1+1}-\frac{1}{n-1+2})$
下図のように打ち消しあっていくので、
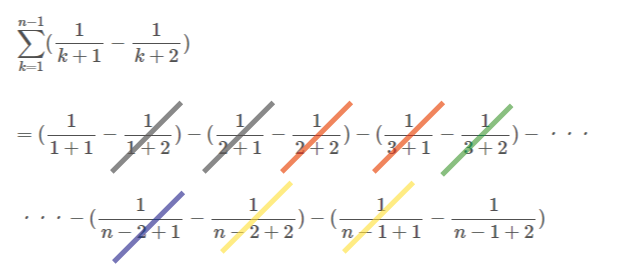
残るのは、
$\displaystyle =\frac{1}{2}-\frac{1}{n+1}$
$\displaystyle =\frac{n+1-2}{2(n+1)}$
$\displaystyle =\frac{1}{2}(\frac{n-1}{n+1})$
$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{k+1}-\frac{1}{k+2}) =\frac{1}{2}(\frac{n-1}{n+1})$・・・( v )
$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{3})^{k+1}$は?
$n$は$2$以上の自然数とするので、
$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{3})^{k+1}$
↑これは初項$\displaystyle \frac{1}{9}$、公比$\displaystyle \frac{1}{3}$、項数$n-1$の和なので、
$\displaystyle \frac{\frac{1}{9}(1-(\frac{1}{3})^{n-1})}{1-\frac{1}{3}}$
※等比数列の和$\displaystyle \sum_{k=1}^{n} ar^{k-1}=\frac{a(1-r^n)}{1-r}$の求め方はこちら>
$\displaystyle \frac{\frac{1}{9}(1-(\frac{1}{3})^{n-1})}{1-\frac{1}{3}}$
$\displaystyle =\frac{\frac{1}{9}(1-(\frac{1}{3})^{n-1})}{\frac{2}{3}}$
$\displaystyle =\frac{1}{6}(1-(\frac{1}{3})^{n-1})$
$\displaystyle =\frac{1}{6}-\frac{1}{6}(\frac{1}{3})^{n-1}$
$\displaystyle (\frac{1}{3})^{n-1}$を$\displaystyle (\frac{1}{3})^{n}$にしたいので、$\displaystyle 3・\frac{1}{3}$を掛ける
※$\displaystyle \frac{1}{3}・(\frac{1}{3})^{n-1}=(\frac{1}{3})^{n}$
$\displaystyle =\frac{1}{6}-3・\frac{1}{3}・\frac{1}{6}(\frac{1}{3})^{n-1}$
$\displaystyle =\frac{1}{6}-\frac{1}{2}(\frac{1}{3})^{n}$
$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{3})^{k+1}=\frac{1}{6}-\frac{1}{2}(\frac{1}{3})^{n}$・・・( vi )
$b_n$は?
( iv )$\displaystyle b_{n+1}-b_n = \frac{1}{n+1}-\frac{1}{n+2} -(\frac{1}{3})^{n+1} $より、
$\displaystyle b_{n+1} = b_n + \frac{1}{n+1}-\frac{1}{n+2} -(\frac{1}{3})^{n+1} $
ここで$\displaystyle c_{n}=\frac{1}{n+1}-\frac{1}{n+2}$、$\displaystyle d_{n}=(\frac{1}{3})^{n+1}$とおくと、
$\displaystyle b_{n}=b_{n-1}+c_{n-1} -d_{n-1}$
同様に$\displaystyle b_{n-1}=b_{n-2}+c_{n-2} -d_{n-2}$なので、
$\displaystyle =b_{n-2}+(c_{n-2}+c_{n-1}) -(d_{n-2} +d_{n-1})$
同様に同じ操作を$n=1$になるまで続けると、
$\displaystyle -(d_{1} +d_{2}+・・・+d_{n-2} +d_{n-1})$
$\displaystyle =b_{1}+\sum_{k=1}^{n-1}(c_{k})-\sum_{k=1}^{n-1}(d_{k})$
$\displaystyle b_1=0$、( v ) $\displaystyle \sum_{k=1}^{n-1}(\frac{1}{k+1}-\frac{1}{k+2}) =\frac{1}{2}(\frac{n-1}{n+1})$、( vi )$\displaystyle \sum_{k=1}^{n-1}(\frac{1}{3})^{k+1}=\frac{1}{6}-\frac{1}{2}(\frac{1}{3})^{n}$より、
$\displaystyle b_{n}=\frac{1}{2}(\frac{n-1}{n+1})-(\frac{1}{6}-\frac{1}{2}(\frac{1}{3})^{n})$
$\displaystyle b_{n}=\frac{1}{2}(\frac{n-1}{n+1})-(\frac{1}{6}-\frac{1}{2}(\frac{1}{3})^{n})$
$\displaystyle =\frac{n-1}{2n+2}-\frac{1}{6}+\frac{1}{2}(\frac{1}{3})^{n}$
$\displaystyle =\frac{3(n-1)-(n+1)}{6n+6}+\frac{1}{2}(\frac{1}{3})^{n}$
$\displaystyle =\frac{2n-4}{6n+6}+\frac{1}{2}(\frac{1}{3})^{n}$
$\displaystyle =\frac{n-2}{3n+3}+\frac{1}{2}(\frac{1}{3})^{n}$
$\displaystyle =\frac{n-2}{3(n+1)}+\frac{1}{2}(\frac{1}{3})^{n}$
$\displaystyle b_{n}=\frac{n-2}{3(n+1)}+\frac{1}{2}(\frac{1}{3})^{n}$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています