
標準偏差の特徴を実際のデータの結果から見てみたいと思います。
標準偏差とは「点数が平均からどれくらい散らばっているかの平均みたいなもの」という感じなので、「平均から散らばっているデータ」と「平均に偏っているデータ」の2つを比較してみたいと思います。
一番身近なテストの点数で考えます。グラフが見やすいので、5点満点のテストにしています。
標準偏差の特徴
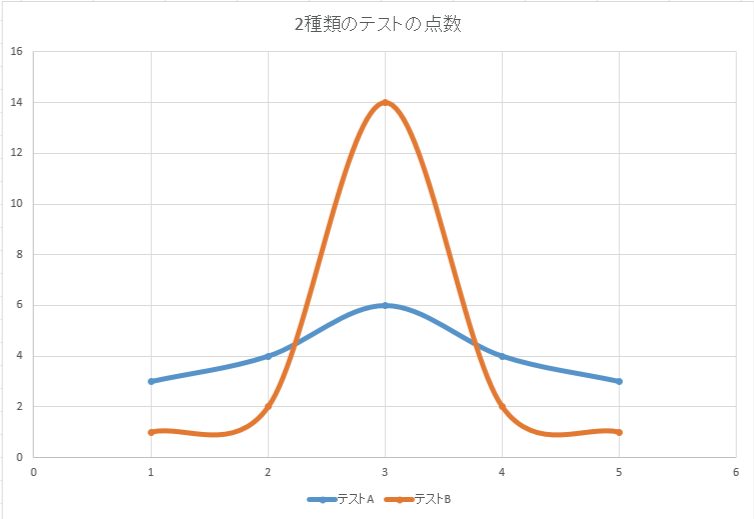
青グラフのテストは平均点から離れている人もそれなりにいる(点数が散らばっている)というテストです。こちらの標準偏差は「1.264911064」です。平均点から1点ちょっと離れている人が多いのかなということが分かります。5点満点のテストでの1点は大きいですよね。
次に、オレンジグラフは平均点あたりの人が多いテストです。こちらの標準偏差は「0.774596669」です。平均点から1点も離れていない人が多い、つまり平均点の人自体多いのかなと考えられます。
このように、平均点から散らばっているとき標準偏差は大きくなり、平均点に近いデータが多いとき標準偏差は小さくなります。
質問です
青グラフのテストで5点取るのと、オレンジグラフのテストで5点取るのはどちらがすごいと思いますか?
平均点から考える
まずは、平均点から考えてみましょう。どちらのテストも平均点は3点です。その中で5点を取るのだから、どちらも同じくらいすごいと思えます。
各点数の人数から考える
では、各点数の人数も比較してみましょう。青グラフのテストは4点が4人、5点が3人います。合わせると7人が8割以上のテストということです。では、オレンジグラフはどうでしょう。
オレンジグラフのテストは4点が2人、5点が1人です。合わせると3人が8割以上のテストということです。
いかがでしょうか?
青グラフのテストは7人も8割以上、オレンジグラフのテストは3人だけが8割以上、どちらのテストも同じくらいの学力の生徒が受けたとすれば、オレンジグラフのテストの方が難しそうではありませんか?
そう考えると、オレンジグラフのテストで5点を取った方がすごいのかなと考えることができます。
この結果は標準偏差とも紐づきます。
標準偏差と紐づく
「青グラフのテストは7人も8割以上、オレンジグラフのテストは3人だけが8割以上」
これを言い換えると、青グラフのテストは平均点から離れた人も多くいるといえます。そして、オレンジグラフのテストは平均点から離れた人が少ないといえます。
標準偏差とは平均との差の平均(みたいなもの)なので、平均点から離れた人も多くいる青グラフの標準偏差は大きくなります。反対に平均点から離れた人が少ないオレンジグラフの標準偏差は小さくなります。
この結果から分かったこと
平均点だけではオレンジグラフの方が難しいとは感じられませんでしたが、標準偏差を比較することで、「オレンジグラフのテストの方が難しいかも」と考えることができるようになります。
標準偏差って平均と比べるとややこしい気がすると思い込んでいましたが、距離が近くなった気がしました。
データ
各データ20人ずつの結果です。平均点は同じ、標準偏差が異なっています。
1つ目のデータ

点数が平均点から散らばっているデータです。まずは、イメージしやすいように何点が何人いたかのグラフです。青色のグラフが1つ目のデータです。緩やかな山になっていますね。
次は実際のデータです。1つ目が20個のデータと合計、平均、標準偏差の表です。分かりにくいと思いますので、何点が何人いるのかの表を続けて載せています。
| 出席番号 | 点数 |
|---|---|
| 1 | 1点 |
| 2 | 1点 |
| 3 | 1点 |
| 4 | 2点 |
| 5 | 2点 |
| 6 | 2点 |
| 7 | 2点 |
| 8 | 3点 |
| 9 | 3点 |
| 10 | 3点 |
| 11 | 3点 |
| 12 | 3点 |
| 13 | 3点 |
| 14 | 4点 |
| 15 | 4点 |
| 16 | 4点 |
| 17 | 4点 |
| 18 | 5点 |
| 19 | 5点 |
| 20 | 5点 |
| 合計 | 60点 |
| 平均 | 3点 |
| 標準偏差 | 1.264911064 |
| 点数 | 人数 |
|---|---|
| 1点 | 3人 |
| 2点 | 4人 |
| 3点 | 6人 |
| 4点 | 4人 |
| 5点 | 3人 |
| 合計 | 60点 |
| 平均 | 3点 |
| 標準偏差 | 1.264911064 |
上の表を見ると、各点数にそれぞれある程度人数がいますね。このようにデータが平均点から散らばっているデータの標準偏差は大きくなります。
「平均点との差の平均(みたいなもの)」が標準偏差なので、「平均点から離れているデータ」が多いのであれば、「平均点との差」も当然大きいものが多くなります。そして、平均をとるデータ「平均点との差」が大きいものが多いということは、平均つまり「標準偏差」も大きくなります。
では、次は平均点に近い点数の人が多いデータです。
2つ目のデータ

点数が平均点からあまり散らばっていないデータです。イメージしやすいように何点が何人いたかのグラフです。オレンジ色のグラフが2つ目のデータです。急激に高くなる山ですね。
次は実際のデータです。1つ目が20個のデータと合計、平均、標準偏差の表です。分かりにくいと思いますので、何点が何人いるのかの表を続けて載せています。
| 出席番号 | 点数 |
|---|---|
| 1 | 1点 |
| 2 | 2点 |
| 3 | 2点 |
| 4 | 3点 |
| 5 | 3点 |
| 6 | 3点 |
| 7 | 3点 |
| 8 | 3点 |
| 9 | 3点 |
| 10 | 3点 |
| 11 | 3点 |
| 12 | 3点 |
| 13 | 3点 |
| 14 | 3点 |
| 15 | 3点 |
| 16 | 3点 |
| 17 | 3点 |
| 18 | 4点 |
| 19 | 4点 |
| 20 | 5点 |
| 合計 | 60点 |
| 平均 | 3点 |
| 標準偏差 | 0.774596669 |
| 点数 | 人数 |
|---|---|
| 1点 | 1人 |
| 2点 | 2人 |
| 3点 | 14人 |
| 4点 | 2人 |
| 5点 | 1人 |
| 合計 | 60点 |
| 平均 | 3点 |
| 標準偏差 | 0.774596669 |
上の表を見ると、平均点の3点が大半です。このようにデータが平均点に寄っている、つまりあまり散らばっていないデータの標準偏差は小さくなります。
「平均点との差の平均(みたいなもの)」が標準偏差なので、「平均点から離れているデータ」が少ないのであれば、「平均点との差」も当然小さいものが多くなります。そして、平均をとるデータ「平均点との差」が小さいものが多いということは、平均つまり「標準偏差」も小さくなります。
まとめ
平均値と同じように標準偏差からも分かることがあります。しかも、平均値だけでは分からなかったことが見えてくることもあります。
毛嫌いせずに理解しようとすることも大切だと改めて感じました。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
標準偏差、平均値



