
単位円とは原点を中心とする半径1の円のことです。
この単位円を使うことで、$\sin$、$\cos$の値を簡単な形で表すことができます。三角比を考える上で非常に便利なツールなので覚えておくことをオススメします。
単位円
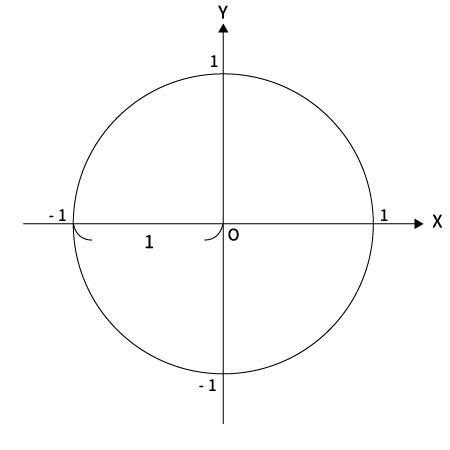
単位円とは下図のように原点$O$を中心とする半径1の円のことです。
単位円に点$P$をとり、直角三角形を作る
単位円の円周上に点$P(x, \, y)$をとり、$X$軸に垂線を下ろします。その垂線と$X$軸との交点をQとすると、$\bigtriangleup OPQ$は直角三角形となります。
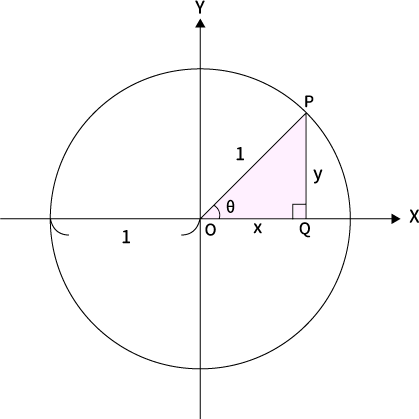
半径$1$なので斜辺も$1$
円の半径は$1$なので、斜辺$PO$も$1$になります。
ここで、$\angle POQ=\theta$とすると、斜辺$PO=1$なので、
$\displaystyle \sin \theta=\frac{y}{1}=y$
$\displaystyle \cos \theta=\frac{x}{1}=x$
となります。
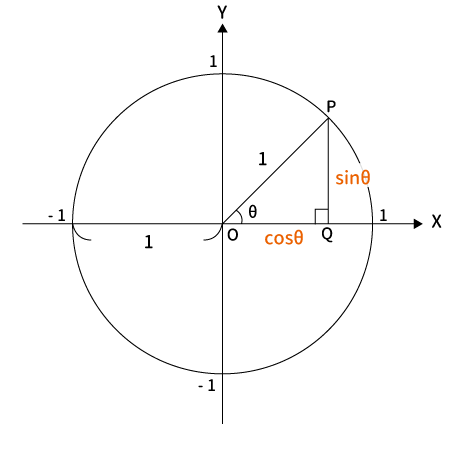
$X$座標$x=\cos \theta$、$Y$座標$y=\sin \theta$なので、点$P$の座標は$(\cos \theta, \, \sin \theta)$になります。
とても便利
$cos$も$sin$も分母は斜辺になります。つまり、単位円の場合であれば斜辺は半径なので$1$です。よって、$cos$の値は$x$座標の値に、$sin$の値は$y$座標の値になります。
単位円のおかげでかなりシンプルな形になります。三角比を考える上で、とても便利なツールですね。
$90^{\circ}<\theta$の場合
$90^{\circ}<\theta$の場合は、直角三角形を作れません。
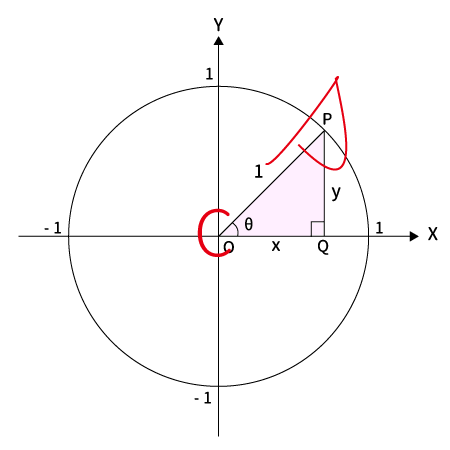
三角形の内角の合計は$180^{\circ}$なので、下図のように$90^{\circ}<\theta$(鈍角)の場合、残り2つの角(赤と青)はどちらも$90^{\circ}$より小さくなるため、直角三角形は作れません。
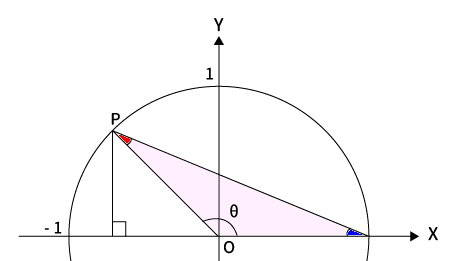
そもそも$180^{\circ}<\theta$の場合は、三角形の内角の和を超えるので三角形すら作れません。
ですので、先ほど見た「$\theta<90^{\circ}$の場合の点$P(\cos \theta, \, \sin \theta)$」を拡張します。
つまり、単位円の円周上の点$P$の$X$座標の値を$\cos \theta$、$Y$座標の値を$\sin \theta$と定義します。定義なのでこれは覚えましょう。単位円から思い出せるようにしておくと良いと思います。
※$(1, \, 0)$を$S$として、$\theta$は$\angle POS$になります
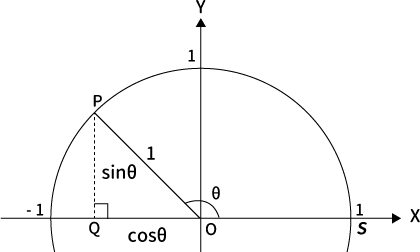
$90^{\circ} < \theta < 180^{\circ}$の場合
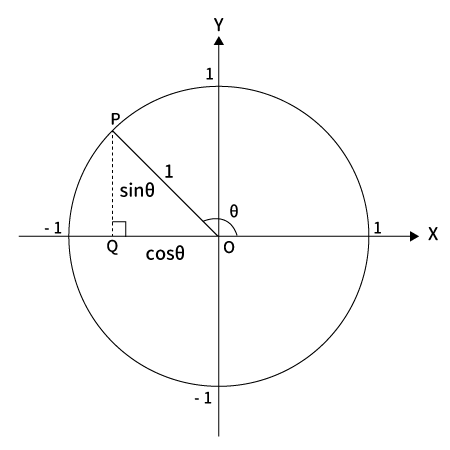
$x = \cos \theta$、$y = \sin \theta$となります。
ここで注目すべきは$cos \theta$の値は負という点です。
$180^{\circ} < \theta < 270^{\circ}$の場合
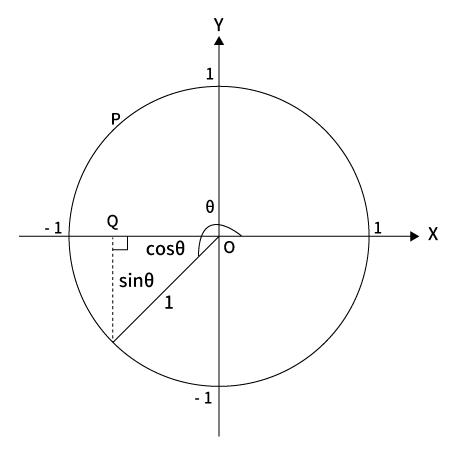
$x = \cos \theta$、$y = \sin \theta$となります。
ここで注目すべきは$cos \theta$、$sin \theta$の値はともに負という点です。
$270^{\circ} < \theta < 360^{\circ}$の場合

$x = \cos \theta$、$y = \sin \theta$となります。
ここで注目すべきは$sin \theta$の値は負という点です。
符号についてまとめると
| $\theta$の範囲 | $\cos \theta$ | $\sin \theta$ |
|---|---|---|
| $0^{\circ}<\theta < 90^{\circ}$ | 正 | 正 |
| $90^{\circ}<\theta < 180^{\circ}$ | 負 | 正 |
| $180^{\circ}<\theta < 270^{\circ}$ | 負 | 負 |
| $270^{\circ}<\theta < 360^{\circ}$ | 正 | 負 |
$\theta$が$0^{\circ},\,90^{\circ},\,180^{\circ},\,270^{\circ}$のとき
これらも同じように考えれば良いので、点$P$の座標をチェックしましょう。
下図のとおりの座標であることがすぐにわかるかと思います。
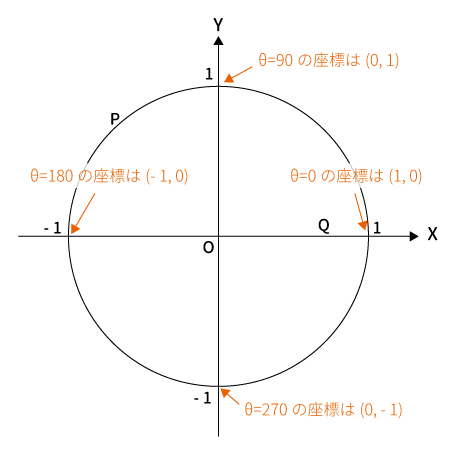
それでは、こちらも表にまとめておきます。
| $\theta$ | $\cos \theta$ | $\sin \theta$ |
|---|---|---|
| $0^{\circ}$ | 1 | 0 |
| $90^{\circ}$ | 0 | 1 |
| $180^{\circ}$ | -1 | 0 |
| $270^{\circ}$ | 0 | -1 |
まとめ
単位円において、$\theta$が$0^{\circ}~360^{\circ}$のときの$\sin \theta$、$\cos \theta$を確認できました。
三角比を考える上でいろいろな特徴も導き出せるので、単位円と三角比の関係は是非覚えておきたいところです。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
単位円、$\sin \theta$、$\cos \theta$、三角比




