
箱ひげ図とは?

↑これが箱ひげ図です。名前のとおり、箱からひげが生えている図ですね。
図の意味
それではどういった意味があるか見てみましょう。
箱ひげ図とは、データの最小値、最大値、四分位数(第1四分位数、第2四分位数(中央値)、第3四分位数、四分位範囲)を図示したものです。それぞれ下記の各箇所から読み取ることができます。
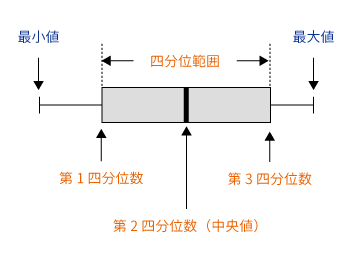
| 左の縦線 | 最小値 |
|---|---|
| 右の縦線 | 最大値 |
| 箱の左端 | 第1四分位数 |
| 箱の右端 | 第3四分位数 |
| 箱の中の縦線 | 第2四分位数(中央値) |
| 箱の長さ | 四分位範囲 |
箱ひげ図の例
学校のあるクラスでテストをしました。生徒が9名で各点数が下記のとおりです。
このデータに対する箱ひげ図を作ってみます。
| Aさん | 80点 |
|---|---|
| Bさん | 76点 |
| Cさん | 55点 |
| Dさん | 62点 |
| Eさん | 92点 |
| Fさん | 78点 |
| Gさん | 58点 |
| Hさん | 65点 |
| Iさん | 88点 |
各項目の値を確認
まずは、必要な値を確認します。
| 最小値 | 55 |
|---|---|
| 最大値 | 92 |
| 第1四分位数 | 60 |
| 第2四分位数(中央値) | 76 |
| 第3四分位数線 | 84 |
| 四分位範囲 | 16 |
四分位数についてはこちら(同じデータを使った具体例があります)>
箱ひげ図作成
それぞれの値を元に箱ひげ図を作成しました。

同じデータを持つグループがあるとき解析に役立つ
下記令和2年度本試験の数1の問題の第4問の(2)などに載っている図1などを見るとイメージしやすいと思います。
平成27年の男の市区町村別平均寿命が47都道府県別に箱ひげ図で図示されています。
都道府県別で平均寿命にどのような特徴があるのか?偏りがあるのか?分析することができます。数値ではなく図(箱ひげ図)で見ることが出来るので、特徴が目に見て分かりやすいです。
他にも
学級別テストの点数などでも箱ひげ図を使えば、テストの難易度が難し過ぎるのか、簡単すぎるのかなど、把握し改善することにも利用できそうです。
データ社会の中でデータを整理し、分析する方法はいくつか知っておいた方が良いのは間違いないと思います。テスト勉強も兼ねて箱ひげ図をぜひ覚えてみてください。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
箱ひげ図、最大値、最小値、四分位数、第1四分位数、第2四分位数、第3四分位数、四分位範囲、データ解析




