内積ってcosを使っても求められるの？

$\overrightarrow {OA} \cdot \overrightarrow{OB}=|\overrightarrow {OA}|  |\overrightarrow{OB}| \cos \angle AOB$

このような公式を見たことがあります。

僕の内積の記憶は、$\overrightarrow {OA} = (a_1, \, a_2)$、$\overrightarrow {OB} = (b_1, \, b_2)$のとき、$\overrightarrow {OA} \cdot \overrightarrow{OB}=a_1 b_1 + a_2 b_2$でした。これを( i ) とおいておきます。

どうして内積が$|\overrightarrow {OA}||\overrightarrow{OB}| \cos \angle AOB$でも表せるのか理解したいと思います。

$|\overrightarrow {OA}|$、$|\overrightarrow{OB}|$

まずは$|\overrightarrow {OA}|$と$|\overrightarrow{OB}|$を確認しておきます。

$|\overrightarrow {OA}|$

これは図で見ると簡単に分かります。

上記より、原点$O$から$A$までの長さ$|\overrightarrow {OA}|$は三平方の定理より、$|\overrightarrow {OA}| = \sqrt{a_1^2 + a_2^2}$・・・( ii )
※$A$の座標はプラスでもマイナスでも2乗するので大丈夫です

$|\overrightarrow {OB}|$

こちらも同様です。これは図で見ると簡単に分かります。

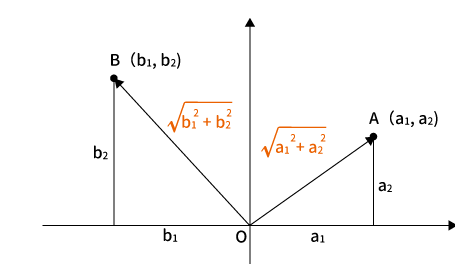
上記より、原点$O$から$B$までの長さ$|\overrightarrow {OB}|$は三平方の定理より、$|\overrightarrow {OB}| = \sqrt{b_1^2 + b_2^2}$・・・( iii )
※$B$の座標はプラスでもマイナスでも2乗するので大丈夫です

$|\overrightarrow {AB}|$

線分$AB$の長さは2通りの方法で表すことができます。

1つは上の$|\overrightarrow {OA}|$、$|\overrightarrow{OB}|$と同じようにベクトル$\overrightarrow {AB}$から求める方法と、図の三角形$OAB$に対して余弦定理を使って求める2通りです。
関連記事：余弦定理の理解を深める

ベクトル$\overrightarrow {AB}$から$|\overrightarrow {AB}|$を求める

$\overrightarrow {AB} = (b_1, \, b_2) – (a_1, \, a_2)$

$= (b_1-a_1, \, b_2-a_2)$

$\overrightarrow {AB} =(b_1-a_1, \, b_2-a_2)$より、

$|\overrightarrow {AB}| = \sqrt{(b_1-a_1)^2 + (b_2-a_2)^2}$

$|\overrightarrow {AB}| = \sqrt{b_1^2 -2a_1 b_1 +a_1^2 + b_2^2 -2a_2 b_2 +a_2^2}$・・・( iv )

余弦定理より$|\overrightarrow {AB}|$を求める

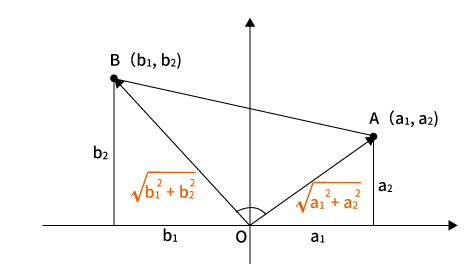
上図より、$|\overrightarrow {AB}|$は余弦定理から求められます。

$|\overrightarrow {AB}|^2 = |\overrightarrow {OA}|^2 + |\overrightarrow{OB}|^2 \, – \, 2|\overrightarrow {OA}||\overrightarrow{OB}|\cos \angle AOB$

$|\overrightarrow {OA}| = \sqrt{a_1^2 + a_2^2}$、$|\overrightarrow {OB}| = \sqrt{b_1^2 + b_2^2}$を代入すると、

$|\overrightarrow {AB}|^2 = a_1^2 + a_2^2 + b_1^2 + b_2^2 \, – \, 2 \sqrt{a_1^2 + a_2^2}\sqrt{b_1^2 + b_2^2} \cos \angle AOB$・・・( v )

( v )に( iv )を代入すると、

$b_1^2 -2a_1 b_1 +a_1^2 + b_2^2 -2a_2 b_2 +a_2^2 $$= a_1^2 + a_2^2 + b_1^2 + b_2^2 \, – \, 2 \sqrt{a_1^2 + a_2^2}\sqrt{b_1^2 + b_2^2} \cos \angle AOB$

$a_1 b_1 +a_2 b_2 = \sqrt{a_1^2 + a_2^2}\sqrt{b_1^2 + b_2^2} \cos \angle AOB$

ここで、( i ) $\overrightarrow {OA} \cdot \overrightarrow{OB}=a_1 b_1 + a_2 b_2$、( ii )$|\overrightarrow {OA}| = \sqrt{a_1^2 + a_2^2}$、( iii )$|\overrightarrow {OB}| = \sqrt{b_1^2 + b_2^2}$より、

$\overrightarrow {OA} \cdot \overrightarrow{OB} = |\overrightarrow {OA}||\overrightarrow {OB}|\cos \angle AOB$

理解しようとしていた公式そのものになりました。

まとめ

一方は三平方の定理から長さを求めて、もう一方は余弦定理から求める。そうすると、内積が各長さとその間の$\cos$の値で求められることが分かりました。

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

ベクトル、内積、余弦定理、三平方の定理、絶対値