余弦定理の理解を深める

余弦定理とは

$\bigtriangleup ABC$ において、$a = BC$, $b = CA$, $c = AB$, $\alpha = \angle CAB$,$ \beta = \angle ABC$,$ \gamma = \angle BCA$ としたとき

$a^2 = b^2 + c^2 − 2bc \cos \alpha$
$b^2 = c^2 + a^2 − 2ca \cos \beta$
$c^2 = a^2 + b^2 − 2ab \cos \gamma$
が成り立つ。これらの式が成り立つという命題を余弦定理、あるいは第二余弦定理という。

ウィキペディアの執筆者，2021，「余弦定理」『ウィキペディア日本語版』，（2021年7月18日取得，https://ja.wikipedia.org/w/index.php?title=%E4%BD%99%E5%BC%A6%E5%AE%9A%E7%90%86&oldid=83837197）．

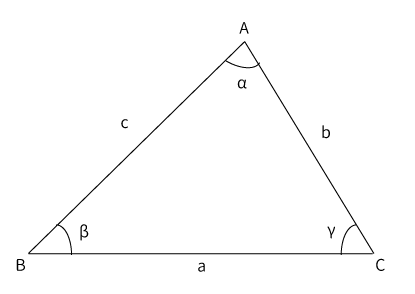
直角三角形であれば2辺が分かれば最後の辺の長さが三平方の定理を使って計算することができます。

では、上図の\bigtriangleup ABC$のように90度が存在しない三角形の場合はどうでしょう？
実はこの場合でも、余弦定理より、2辺とその間の$\cos$の値が分かれば、もう一辺の長さを計算することができるんです。

なぜ、「2辺の長さ」と「その間の$\cos$の値」を使った式で、最後の辺の長さを表せるのでしょうか？

実際に余弦定理を導いて理解を深めましょう。

余弦定理を得られるまでの流れの理由・意味を知ることで、忘れたときでも思い出すきっかけになると思います。”いざ”というときのために、余弦定理の導き方まで覚えてしまいましょう

$b^2 = a^2 + c^2 − 2ac \cos \beta$を三平方の定理から導く

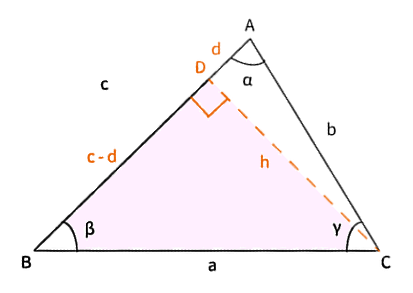
$\bigtriangleup ABC$の$A$から$BC$に垂線を引きます。$BC$との交点を$D$とします。

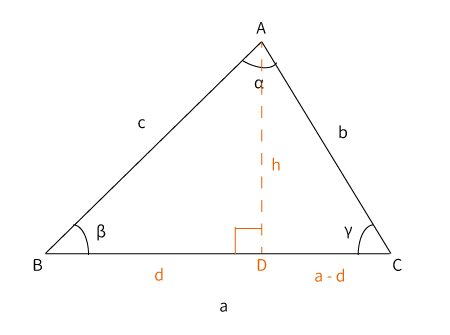
また、$AD=h$、$BD=d$とします。

$\bigtriangleup ABD$は直角三角形

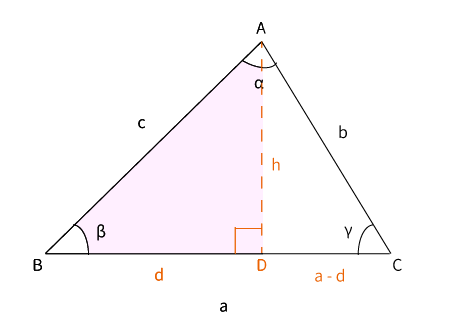
$\bigtriangleup ABD$は直角三角形なので三平方の定理より、$c^2=d^2+h^2$・・・( i )が成り立ちます。

また、同様に$\bigtriangleup ABD$は直角三角形なので$\displaystyle \cos \beta$の値が分かります。

$\displaystyle \cos \beta  = \frac{d}{c}$も成り立ちます。

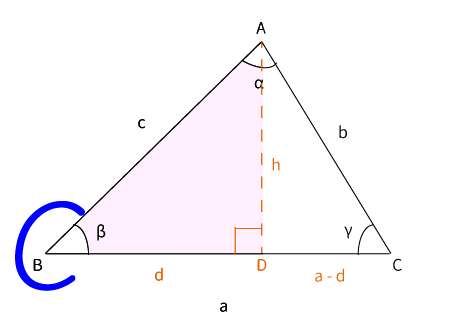
両辺に$c$を掛けて、左辺と右辺を入れ替えると、$d = c\cos \beta$・・・ ( ii )

これによって、「$c$と$\beta$」で$d$を表すことができました。

$\bigtriangleup ADC$も直角三角形

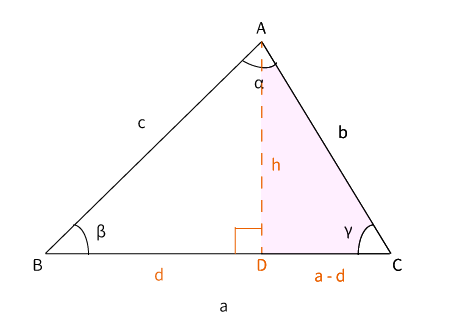
$\bigtriangleup ADC$も直角三角形なので三平方の定理より、$b^2=(a-d)^2+h^2$・・・( iii )が成り立ちます。

$h$を消す

ここで、( i ) $c^2=d^2+h^2$、( iii )$b^2=(a-d)^2+h^2$ ともにh^2があるので、( i ) – ( iii )をして$h^2$を消します。

$c^2 – b^2 = d^2 – (a-d)^2$

下記のように変形しました。

$c^2 – b^2 = -a^2+2ad$・・・( iv )

$d$を消す

上記( iv )に ( ii ) $d = c\cos \beta$を代入すると、
$c^2 – b^2 = -a^2+2ca\cos \beta$

$b^2 = c^2+a^2-2ca\cos \beta$

三平方の定理から余弦定理の一つ$b^2 = a^2+c^2-2ac\cos \beta$を導くことができました。

続けて$c^2 = a^2 +b^2- 2ab\cos \gamma$を導く

次に$cos \gamma$の値を見てみましょう。

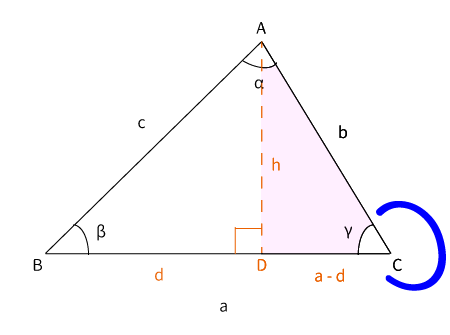
$\bigtriangleup ADC$は直角三角形なので$\displaystyle \cos \gamma$の値が分かります。

$\displaystyle \cos \gamma = \frac{a-d}{b}$が成り立ちます。

下記のように変形しました。
$d = a – b\cos \gamma$

これを先ほどの( iv )$c^2 – b^2 = -a^2+2ad$に代入すると、

$c^2 – b^2 = -a^2+2a(a – b\cos \gamma)$

$c^2 = a^2 +b^2- 2ab\cos \gamma$

三平方の定理から余弦定理の一つ$c^2 = a^2 +b^2- ab\cos \gamma$を導くことができました。

$a^2 = b^2 + c^2 − 2bc \cos \alpha$を三平方の定理から導く

 

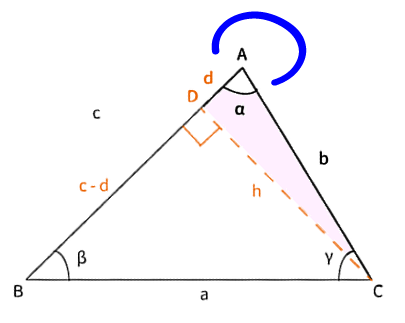
$\bigtriangleup ABC$の$C$から$AB$に垂線を引きます。$AB$との交点を$D$とします。

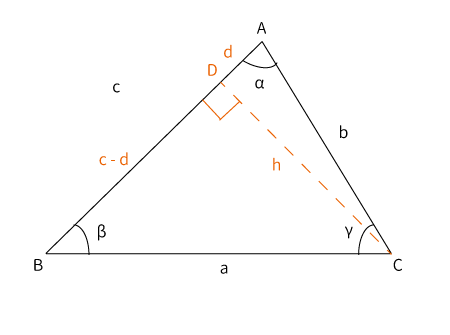
また、$CD=h$、$AD=d$とします。

$\bigtriangleup ADC$は直角三角形

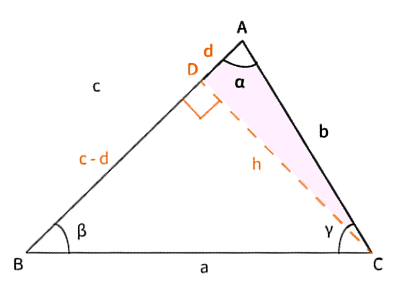
$\bigtriangleup ADC$は直角三角形なので三平方の定理より、$b^2=d^2+h^2$・・・( i )が成り立ちます。

また、同様に$\bigtriangleup ADC$は直角三角形なので$\displaystyle \cos \alpha$の値が分かります。

$\displaystyle \cos \alpha = \frac{d}{b}$も成り立ちます。

両辺に$b$を掛けて、左辺と右辺を入れ替えると、$d = b\cos \alpha$・・・ ( ii )

これによって、「$b$と$\alpha$」で$d$を表すことができました。

$\bigtriangleup DBC$も直角三角形

$\bigtriangleup DBC$も直角三角形なので三平方の定理より、$a^2=(c-d)^2+h^2$・・・( iii )が成り立ちます。

$h$を消す

ここで、( i ) $b^2=d^2+h^2$、( iii )$a^2=(c-d)^2+h^2$ ともにh^2があるので、( i ) – ( iii )をして$h^2$を消します。

$b^2 – a^2 = d^2 – (c-d)^2$

下記のように変形しました。

$b^2 – a^2 = -c^2+2cd$・・・( iv )

$d$を消す

上記( iv )に ( ii ) $d = b\cos \alpha$を代入すると、

$b^2 – a^2 = -c^2+2bc\cos \alpha$

$a^2 = b^2+c^2-2bc\cos \alpha$

三平方の定理から余弦定理の最後の一つ$a^2 = b^2+c^2-2bc\cos \alpha$を導くことができました。

まとめ

下記のように各頂点から各辺に垂線を下ろすことで、2辺とその間の角の$cos$の値で残りの1辺を導くことができます。

上記で実際に計算した結果、余弦の定理を導くことができました。

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

余弦定理、三平方の定理