メラネウスの定理？図を用いて分かりやすく証明

メラネウスの定理とは、三角形と線との関係性の定理です。

$\bigtriangleup ABC$と線$l$があります。

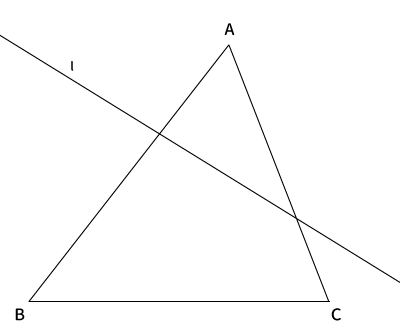
下図のように$BC$を通る直線と直線$l$との交点を$D$、$AC$と直線$l$との交点を$E$、$AB$と直線$l$との交点を$F$とします。

このとき、$\displaystyle \frac{AF}{BF} \frac{BD}{CD} \frac{CE}{AE} = 1$となります。これがメラネウスの定理です。

では、なぜ$\displaystyle \frac{AF}{BF} \frac{BD}{CD} \frac{CE}{AE} = 1$の式が成り立つか証明したいと思います。不明点があれば、お気軽にコメントください。

なんとなく流れが分かっている方が分かりやすいかと思いますので、まずはざっくりとした流れから。

証明のざっくりとした流れ

$\bigtriangleup ABC$の各頂点から直線$l$に対して、垂線を引くと、

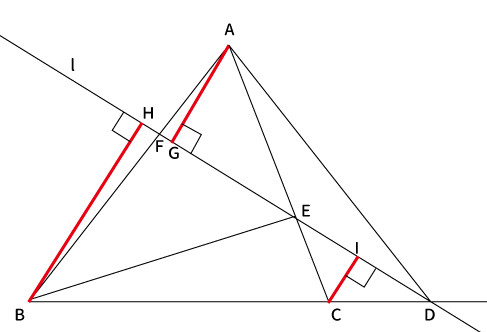
↓この2つの三角形とか、

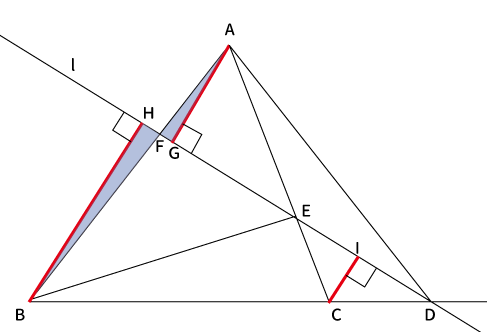
↓この2つの三角形とか、

↓この2つの三角形とかが、それぞれ相似になっていて、

比を考えると、$BH:AG=BF:AF$、$CI:BH=CD:BD$、$AG:CI=AE:CE$になって、それぞれ分数の形にしたものを掛け合わせると、なんとメネラウスの定理の形になります。

それでは、詳しく見ていきます。

メネラウスの定理の証明

まず、$\bigtriangleup ABC$の各頂点から直線$l$に対して、垂線を引きます。

各頂点$A$、$B$、$C$から下ろした垂線と直線$l$との交点をそれぞれ$G$、$H$、$I$とします。

$\bigtriangleup BFH$と$\bigtriangleup AFG$

下記より、$\bigtriangleup BFH$と$\bigtriangleup AFG$は2角が等しいので、2つの三角形は相似な図形です。

• $\angle BHF$と$\angle AGF$はともに$90^{\circ}$
• $\angle BFH$と$\angle AFG$は対頂角（向かい合う角）なので、等しい

よって、辺の比が$BH:AG=BF:AF$となり、$BH・AF=AG・BF$となるので、$\displaystyle \frac{AF}{BF}=\frac{AG}{BH}$という関係式が得られました。

$\bigtriangleup CDI$と$\bigtriangleup BDH$

下記より、$\bigtriangleup CDI$と$\bigtriangleup BDH$は2角が等しいので、2つの三角形は相似な図形です

• $\angle CID$と$\angle BHD$はともに$90^{\circ}$
• $\angle CDI$と$\angle BDH$は同じ角なので、等しい

よって、辺の比が$CI:BH=CD:BD$となり、$CI・BD=BH・CD$となるので、$\displaystyle \frac{BD}{CD}=\frac{BH}{CI}$という関係式が得られました。

$\bigtriangleup AEG$と$\bigtriangleup CEI$

下記より、$\bigtriangleup AEG$と$\bigtriangleup CEI$は2角が等しいので、2つの三角形は相似な図形です

• $\angle AGE$と$\angle CIE$はともに$90^{\circ}$
• $\angle AEG$と$\angle CEI$は対頂角（向かい合う角）なので、等しい

よって、辺の比が$AG:CI=AE:CE$となり、$AG・CE=CI・AE$となるので、$\displaystyle \frac{CE}{AE}=\frac{CI}{AG}$という関係式が得られました。

3つの相似関係より

3つの相似関係より、3つの関係式が得られました。

$\displaystyle \frac{AF}{BF}=\frac{AG}{BH}$・・・( i )

$\displaystyle \frac{BD}{CD}=\frac{BH}{CI}$・・・( ii )

$\displaystyle \frac{CE}{AE}=\frac{CI}{AG}$・・・( iii )

これら3つの両辺をそれぞれ掛け合わせます。( i )$\times$ ( ii )$\times$ ( iii )

（右辺）がきれいに消えて、$1$となるので、

$\displaystyle \frac{AF}{BF}・\frac{BD}{CD}・\frac{CE}{AE}=1$

メネラウスの定理が成り立つことが証明できました。

以上、証明終わります。

まとめ

直線$l$に垂線を引くことで、掃除関係の三角形が作れます。それらの比率を使うことで、メネラウスの定理を証明することができました。

メネラウスの定理はチェバの定理とあわせて覚えておきたいですね。

スポンサーリンク

キーワード

気になる人は調べてみてね。

メネラウスの定理、三角形、相似、対頂角、チェバの定理