平行移動の公式の証明

平行移動の公式

平行移動がどのような感じかイメージしたい方はこちらもご覧ください。

1次方程式 y=ax+b の平行移動 >

平行移動の公式の証明

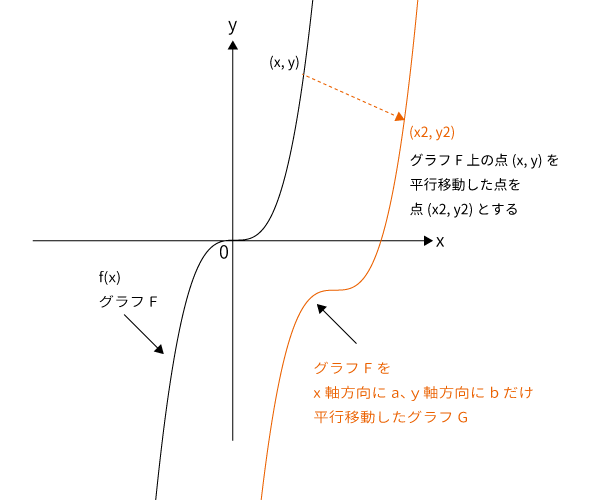
任意の$F$をグラフに持つ$y=f(x)$を$x$軸方向に$\color{red}a$、$y$軸方向に$\color{blue}b$平行移動したグラフを$G$とします。

このとき、グラフ$F$上の任意の点$(x, \, y)$に対応するグラフ$G$上の点を$(x2, \, y2)$とする。

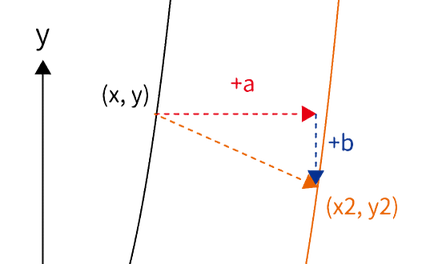
グラフG上の点$(x2, \, y2)$は点$(x, \, y)$を$x$軸方向に$\color{red}a$、$y$軸方向に$\color{blue}b$平行移動した点なので、点$(x+a, \, y+b)$のことである。よって、点$(x2, \, y2)=$点$(x+a, \, y+b)$なので、下記が成り立つ。

$x2=x+a$・・・( i )
$y2=y+b$・・・( ii )

( i ) より、$x=x2-a$・・・( iii )
( ii ) より、$y=y2-b$・・・( iv )

$y=f(x)$に( iii ) ( iv )を代入すれば、グラフFを平行移動したグラフGが持つ関数となる。

$y2-b=f(x2-a)$

これは平行移動の公式になっている。

証明終了。

補足：x2、y2が気持ち悪い

先ほど証明の最後で出てきた、$y2-b=f(x2-a)$。

$y=f(x)$みたいに$x$、$y$となっていないので少し気持ち悪いと感じる人もいるかもしれません。ですが、$x$、$y$、$x2$、$y2$、どれもただの文字です。どちらも意味合いは同じです。

関数とは？（イメージとして）

$y=f(x)$とは、$x$に何か値を渡すと$y$という値を返してくれる装置です。

例えば、「$f(x)=x$」であれば、$x=1$を渡せば$y=1$を、$x=3$を渡せば$y=3$を返してくれます。「$f(x)=x-2$」であれば、$x=1$を渡せば$y=1$を、$x=3$を渡せば$y(=3^2)=9$を返してくれます。

この変換してくれる装置を関数といいます。

関数について少し掘り下げる

関数とは数の集合を値にとる写像の一種です。

集合 A の各元に対してそれぞれ集合 B の元をただひとつずつ指定するような規則 f が与えられているとき、f を「定義域（あるいは始域） A から終域 B への写像」といい

${\displaystyle f\colon A\to B,\quad A{\stackrel {f}{{}\to {}}}B}f\colon A\to B,\quad A{\stackrel {f}{{}\to {}}}B$

などと表す。

ウィキペディアの執筆者，2021，「写像」『ウィキペディア日本語版』，（2021年7月14日取得，https://ja.wikipedia.org/w/index.php?title=%E5%86%99%E5%83%8F&oldid=83243785）．

上で引用した$f$がまさに関数です。

関数・写像の例

下記を例に関数・写像を見てみます。

• 規則$f$が$f(x)=2x$
• 定義域（$x$の範囲）が$-2 \leq x \leq 3$（$x$は整数）
  ※集合が確認しやすいので整数にしています

定義域より、集合$A$は$\{-2, \, -1, \,0, \,1, \,2, \,3\}$です。

集合$A$の各元を規則$f$で変換すると、集合$B$がわかります。

規則$f$は「渡された値を2倍にする」なので、集合$B$は$\{-4, \, -2, \,0, \,2, \,4, \,6\}$となります。

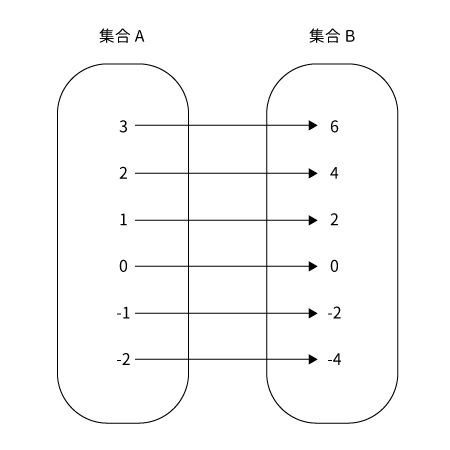
集合Aの各元に対してそれぞれ集合Bの元をただ一つずつ指定するようになっています。このとき$f$を定義域Aから終域Bへの写像といいます。

スポンサーリンク

キーワード

気になる人は調べてみてね。

平行移動の公式、平行移動、グラフ、関数、写像、定義域、終域