
問題
問題は下記を開いてご確認ください。
第5問
$AB$の値を求める
4点$B$、$D$、$F$、$G$が同一円周上にあり、$FD=1$なので下図のようになる。
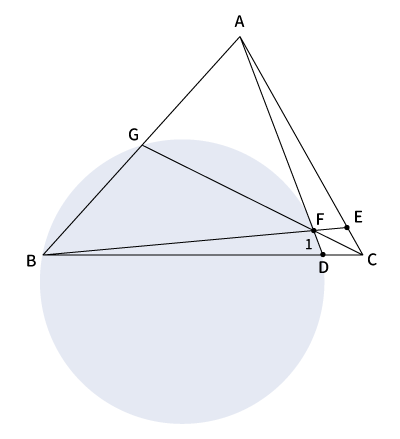
前回求めたとおり$\displaystyle \frac{FD}{AF}=\frac{1}{8}$なので、$FD=1$の場合$\displaystyle \frac{1}{AF}=\frac{1}{8}$となり$AF=8$となる。
また、$FS=1$、$AF=8$より$AD=8+1=9$である。
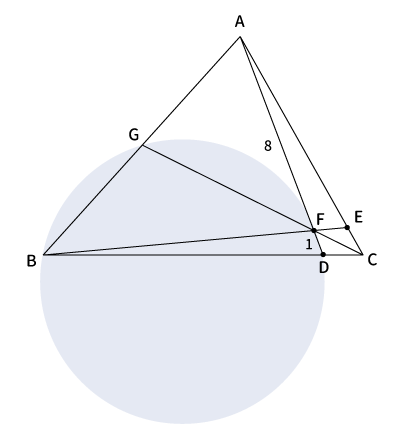
$\angle AFG$と$\angle CFD$は対頂角なので等しい。(※$\angle ●$)
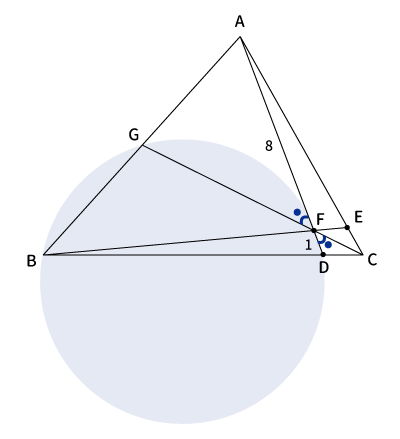
円に内接する四角形の内角は対角の外角と等しくなるので、$\angle AFG=\angle ABD$。(※$\angle ●$)
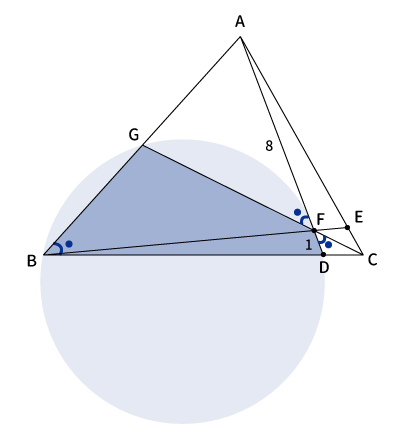
$\angle FAG$と$\angle BAD$は共通の角なので等しい。(※$\angle ▲$)
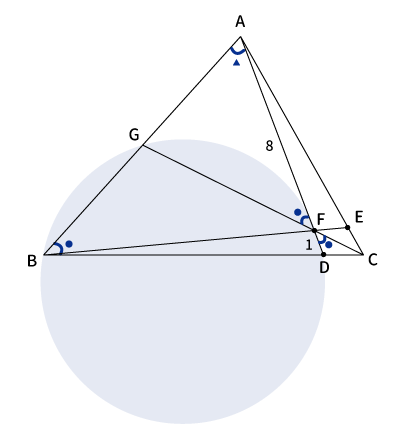
以上より、$\bigtriangleup AFG$と$\bigtriangleup ABD$は2組の角が等しいので、相似である。
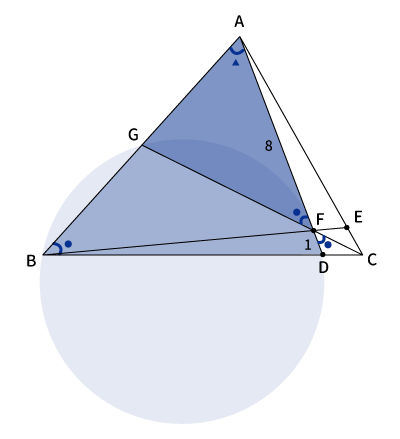
対応する辺は$AF$と$AB$、$AG$と$AD$、$FG$と$BD$なので、$AF:AB=AG:AD$となり、$AB・AG=AF・AD$。
$AF=1$、$AD=9$を代入すると、$AB・AG=AF・AD=8・9=72$・・・( i )※最後の問題で使用
また、前回求めたとおり$\displaystyle \frac{AG}{AB}=\frac{1}{2}$なので、$\displaystyle AG=\frac{1}{2}AB$。
これも代入すると、$\displaystyle AB・\frac{1}{2}AB=72$
$\displaystyle AB・\frac{1}{2}AB=72$
$\displaystyle \frac{AB^2}{2}=72$
$\displaystyle AB^2=144$
$\displaystyle AB=\pm 12$
$\displaystyle AB=\pm 12$。$AB$は辺の長さなので正の数。よって$\displaystyle AB=12$
$AE・AC$を求める
$AE:CE=7:1$なので、全体の辺$AC$の比は$8$となる。よって、$AE:AC=7:8$である。
$AE=3\sqrt{7}$とすると、$3\sqrt{7}:AC=7:8$
$3\sqrt{7}:AC=7:8$
$\displaystyle 7AC=3\sqrt{7} \times 8$
$\displaystyle AC=\frac{24\sqrt{7}}{7}$
$\displaystyle AC=\frac{24\sqrt{7}}{7}$
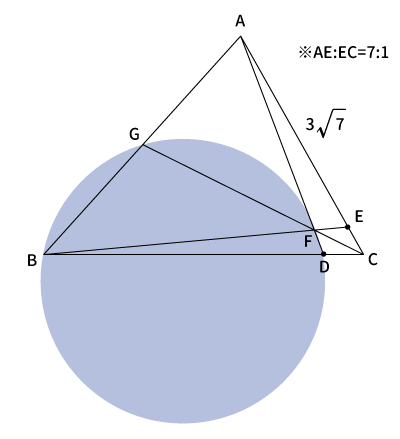
$AC$が求まり、$AE=3\sqrt{7}$なので、
$\displaystyle AE・AC = 3\sqrt{7} \times \frac{24\sqrt{7}}{7}$
$AE・AC = 72$・・・( ii )※最後の問題で使用
$\angle AEG$を求める
( i ) $AB・AG=72$、( ii ) $AE・AC = 72$より、どちらも同じ値なので、$AB・AG= $AE・AC$である。
この式を満たす。つまり四角形$GBCE$は方べきの定理(2つ目)を満たす。よって、四角形$GBCE$は円に内接する四角形である。

$\angle AEG$は$\angle CEG$の外角なので、$\angle ABC$と等しい。
※円に内接する四角形の内角は対角の外角と等しくなるため

スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています