
等差数列の和の公式覚えていますか?
初項$a$、公差$d$、項数$n$が分かっている場合は、
$\displaystyle \sum_{k=1}^{n} \{ a+(n-1)d \}=\frac{1}{2} n \{ 2a + (n-1) d \}$
また、初項$a$、末項$l$、項数$n$が分かっている場合は、
$\displaystyle \sum_{k=1}^{n} a_n=\frac{1}{2} n \{ a + l \}$
これが公式です。一定期間であれば覚えておくことができますが、使わないと忘れていきます。
実はこの公式の求め方はとても簡単です。なので、後でも思い出しやすくするために、「どのように導くか」を覚えておきましょう。その方が、テスト中にど忘れしてしまったときでも思い出せる可能性は高くなると思います。
等差数列の和の公式の求め方
初項$a$、公差$d$、項数$n$が分かっている場合
初項が$a$、公差が$d$の等差数列$a_n=a+(n-1)d$について考えます。
$n=1$であれば、$a_1=a+{1-1}d=a+0=a$、初項はちゃんと$a$ですね。$n=2$であれば、$a_2=a+{2-1}d=a+d$、初項に公差を足した値ですね。公差も問題なさそうです。
$\displaystyle \sum_{k=1}^{n} \{a+(n-1)d\}$$\displaystyle =\frac{1}{2} n \{ 2a + (n-1) d \}$を分解
まず、$a_n=a+(n-1)d$の$1$から$n$までの和$\displaystyle \sum_{k=1}^{n} \{a+(n-1)d\}$を分解します。
( i )と( i )を足す
( i )と( i )を足しますが、少し工夫します。1つ目の ( i ) はそのまま、2つ目の ( i ) は順番をひっくり返したものを用意します。下記を御覧ください。上がそのまま、下がひっくり返したものです。

よって、
$\displaystyle \cdots +\{ 2a + (n-1)d\}+\{ 2a + (n-1)d\}$
右辺の$\{ 2a + (n-1)d\}$は$n$個なので、
最後に両辺$2$で割ると、等差数列の和の公式が求まります。
(余談)本当に各項は$2a + (n-1)d$となる?
$\displaystyle \sum_{k=1}^{n} \{a+(n-1)d\}=(a + 0) + (a + d) + \cdots +\{ a + (n-2)d\}+\{ a + (n-1)d\}$
は等差数列なので、当たり前ですが、公差$d$ずつ増えていきます。
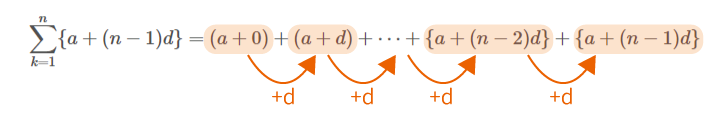
次に上の式をひっくり返した場合は、反対に公差$d$ずつ減っていきます。
$\displaystyle \sum_{k=1}^{n} \{a+(n-1)d\}=\{ a + (n-1)d\} + \{ a + (n-2)d\} + \cdots +(a + d)+(a + 0)$
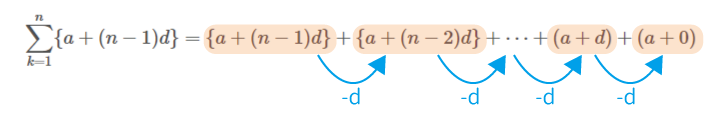
よって、この2式を足すと、$+d$と$-d$ですべて打ち消しあいます。つまり、どちらも一番左の項から変わらないということになります。従って、各項はすべて$(a+0)+\{ a + (n-1)d\} =2a+(n-1)d\$となります。
初項$a$、末項$l$、項数$n$が分かっている場合
「初項$a$、公差$d$、項数$n$が分かっている場合」の途中の式 ( ii ) $\displaystyle 2\sum_{k=1}^{n} \{a+(n-1)d\}$$=n\{ 2a + (n-1)d\}$があります。この式の$2a + (n-1)d$部分が1番目の項と最後の項を足したものになります。
つまり、今回の場合、初項$a$、末項$l$なので、$2a + (n-1)d$部分を$a+l$に置き換えればよいわけです。今回、等差数列の公差が分かっていない状態なので、等差数列は$a_n$として、$2a + (n-1)d = a+l$を代入すると、
$\displaystyle 2\sum_{k=1}^{n} a_n=n\{ a+l\}$
こちらも最後に両辺$2$で割ると、もう一つの等差数列の和の公式が求まります。
$\displaystyle \sum_{k=1}^{n} a_n=\frac{1}{2} n\{ a+l\}$
まとめ
解き方は同じ式の項の順番だけ反対にしただけです。階乗とかの値を求めるとき、つまり、$1$~$10$の合計を求めよなどで見かけるかなと思います。等差数列の和の公式の求め方を覚えておいて、いざというときに備えましょう。
単純に公式を覚えるより、少しでも意味がある方が記憶には残りやすいので是非自分で求められるようにしてみてください。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
等差数列、等差数列の和



