令和2年センター本試＞数１＞第2問 [1] 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第２問 [1]（１）

$y$軸との共有点を持つか調べる

$F$と$y$軸が共有点を持つかを調べる。そのためには、$x=0$を考えればよい。

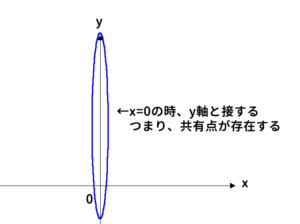
$y=x^2+ax+b=b$となる。よって、$x=0$のとき、$y=b$で必ずy軸と接するので、Fとy軸は共有点を持つ。
よって、$a^2 > 4b$のとき、Fとy軸は共有点をもたない（選択肢：4）、$a^2 < 4b$のとき、Fとy軸は共有点をもたない（選択肢：5）、は正しくない。

$x$軸との共有点を持つか調べる

$F$と$x$軸が共有点を持つかを調べる。そのためには、$y=0$を考えればよい。

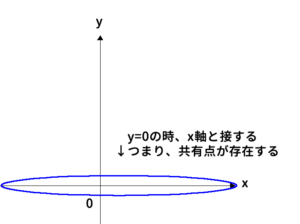
$y=0$のときなので、
$\displaystyle 0=x^2+ax+b$となる。

$y=0$のとき$x$の値がどうなるか知りたいので、解の公式より、
$\displaystyle x=\frac{-a \pm \color{red} \sqrt{a^2 -4b } \color{black}}{2}$

$y=0$のとき、$x$が実数の値を持つには、$\sqrt{\,\,\,}$内が$0$または正の数である必要がある。
※$\sqrt{\,\,\,}$内が負の数になる実数は存在しない（虚数になる）

よって、$a^2-4b \geq 0$のとき、Fとx軸は共有点を持つ。つまり、$a^2-4b < 0$のときFとx軸は共有点を持たない。

不等式の両辺に$4b$を足すと、$a^2 < 4b$となり、このときFとx軸は共有点を持たない（選択肢：３）。

どのような放物線か？

$y=x^2+ax+b$の$b$とは、$y$軸方向に$b$の値分ずらすだけで、グラフの形には何ら影響を与えない。

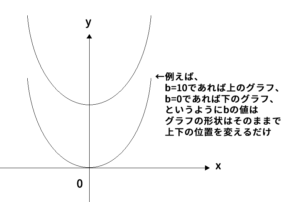
よって、$y=x^2+ax$がどのような放物線かを考える。

$x$軸と交わる点

$y=x^2+ax=x(x+a)$なので、$x=0$、$x=-a$のときに$y=0$になることが分かる。

$x$軸と交わる点の中点

では、その中点である$\displaystyle x=- \frac{a}{2}$を考える。

$\displaystyle y=(-\frac{a}{2})^2-a\frac{a}{2} =\frac{a^2}{4}-\frac{a^2}{2}=-\frac{a^2}{4}$

$a^2$は正なので、$\displaystyle -\frac{a^2}{4}$は負である。よって、中点は$x$軸と交わる点より下になる。

これで、$y=x^2+ax$が下記3点を通ることが分かった。

$(-a, \, 0)$、$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4})$、$(0, \, 0)$

（試しに）$x$軸と交わる点の外側

$x$軸と交わる点から$a$分外側の点をチェックする。

$x=-2a$の場合、

$x=a$の場合、
$y=x^2+ax=a^2+a\times a=2a^2$

さらに、$a$分外側の点をチェックする。

$x=-3a$の場合、

$x=2a$の場合、

$x=-2a$、$x=a$の場合、ともに$y=2a^2$、$x=-3a$、$x=2a$の場合、ともに$y=6a^2$となることが分かった。

この結果から、中点を軸に左右対称であることが推測できる。

任意の実数$t$で考える。

中点から$t$（$t$は任意の実数）だけ$x$軸方向にずらした点を考える

中点から$t$だけ左右にずらした点なので、$\displaystyle x=-\frac{a}{2}+t$、$\displaystyle x=-\frac{a}{2}-t$の2点を考える。

$\displaystyle x=-\frac{a}{2}+t$の場合

$\displaystyle y=x^2+ax$

$\displaystyle =(-\frac{a}{2}+t)^2+a(-\frac{a}{2}+t)$

$\displaystyle =\frac{a^2}{4}-at+t^2-\frac{a^2}{2}+at$

$\displaystyle =-\frac{a^2}{4}+t^2$

$\displaystyle x=-\frac{a}{2}-t$の場合

$\displaystyle y=x^2+ax$

$\displaystyle =(-\frac{a}{2}-t)^2+a(-\frac{a}{2}-t)$

$\displaystyle =\frac{a^2}{4}+at+t^2-\frac{a^2}{2}-at$

$\displaystyle =-\frac{a^2}{4}+t^2$

$\displaystyle x=-\frac{a}{2}+t$、$\displaystyle x=-\frac{a}{2}-t$の場合、ともに$\displaystyle y=-\frac{a^2}{4}+t^2$となることが分かり、中点を軸に左右対称であることが分かった。

下に凸の放物線

上記より、中点（頂点）が$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4})$。

中点を軸にずらした点は$\displaystyle (-\frac{a}{2}-t, \, -\frac{a^2}{4}+t^2)$、$\displaystyle (-\frac{a}{2}+t, \, -\frac{a^2}{4}+t^2)$となることが分かった。

ここで、$a$は定数なので、$\displaystyle -\frac{a^2}{4}$も定数である。よって、$\displaystyle -\frac{a^2}{4}+t^2$は$t^2$を$\displaystyle -\frac{a^2}{4}$（定数）だけ$y$軸方向にずらしただけのグラフだと分かった。

$t^2$は下に凸の放物線なので、$y=x^2+ax$も同様に下に凸の放物線である（選択肢：１）。

$x$軸との共有点を持つか調べる（別解）※こちらの方が正統

上記「どのような放物線か？」より、$y=x^2+ax$は頂点$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4})$の下に凸の放物線である。

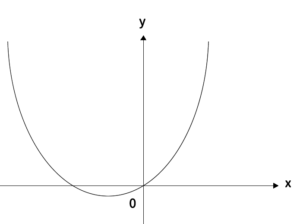
つまり、$y=x^2+ax$に$b$を加えた$y=x^2+ax+b$（グラフ$F$）の頂点は$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4}+b)$となる。ここで頂点の$y$座標が$\displaystyle -\frac{a^2}{4}+b$が$0$より大きくなる場合、このグラフ$F$は$y$軸と共有点を持たない。

よって、$\displaystyle -\frac{a^2}{4}+b>0$の場合、すなわち$\displaystyle 4b>a^2$のとき、$F$と$x$軸は共有点をもたない（選択肢：３）。

解いた結果、少し整理し直した回答はこちら

第２問 [1]（２）

第２問 [1]（１）より、$y=x^2+ax+b$の頂点は$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4}+b)$となる。よって、$y=x^2+2x-1$の場合は、$a=2,b=-1$なので頂点$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4}+b)$は$(-1,  \, -2)$となる。

下に凸な放物線で、頂点$(-1,  \, -2)$は$-3\leq x \leq 2$の範囲にあるので、最小値は$-2$となる。

また、放物線なので、頂点からより離れている方が$y$の値は大きくなる。よって、$x=2$のとき最大値になる。

$y=x^2+2x-1=2^2+2\times 2-1=7$

よって、最小値は$-2$、最大値は$7$となる（選択肢：６）。

スポンサーリンク