令和2年センター本試＞数１＞第3問 (2) ( i ) ( ii ) 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第３問（２）

一先ず、1辺の長さが$8$の正方形$DEFG$において、辺$EF$上の点$H$と辺$FG$上の点$I$は$\displaystyle cos \angle DIG=\frac{3}{5}$、$tan \angle FIH=2$を満たす図形を描く。

$\displaystyle cos \angle DIG=\frac{3}{5}$より、$DI=5x$、$GI=3x$と置き、$tan \angle FIH=2$より、$FI=y$、$HF=2y$と置く。

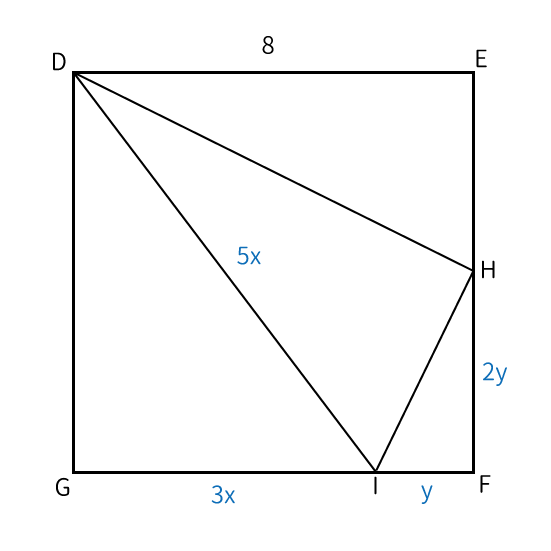
( i ) $DI$、$HI$を求める

$DI$を求める

$\bigtriangleup DIG$、三平方の定理より、$GD^2+IG^2=DI^2$

$GD=8$、$IG=3x$、$DI=5x$なので、$8^2+(3x)^2=(5x)^2$

$x=\pm 2$

ただし、$x$は三角形の辺なので正の数なので$x=2$

$DI=5x$に$x=2$を代入すると、$DI=5\times 2=10$

$DI=10$（選択肢：３）

$HI$を求める

上記「$DI$を求める」より、$x=2$である。

よって、$GI=3 \times 2=6$なので、$y=8-6=2$である。

$\bigtriangleup HIF$、三平方の定理より、$IF^2+FH^2=HI^2$

$IF=2$、$FH=4$なので、$2^2+4^2=HI^2$

$HI=\pm 2\sqrt{5}$

ただし、$HI$は三角形の辺なので正の数である。
よって、$HI=2\sqrt{5}$（選択肢：１）

( ii )相似なもの & 角度の大小を求める

$\bigtriangleup DEH$、$\bigtriangleup DGI$、$\bigtriangleup DHI$の中で$\bigtriangleup HFI$と相似なものは？

まず、「( i ) $DI$、$HI$を求める」で分かった値と$DH$の値を書き込んだ図を作図する。

$DH$の求め方

$DH$は、$\bigtriangleup DEH$、三平方の定理より、

$DH^2=DE^2+EH^2$

$DH=4\sqrt{5}$

$\angle DHI=90^{\circ}$

$DH^2+DI^2=ID^2$を満たすので、$\angle DHI=90^{\circ}$となる。

$ID^2=10^2=100$

$\bigtriangleup DEH$と$\bigtriangleup HFI$は相似？

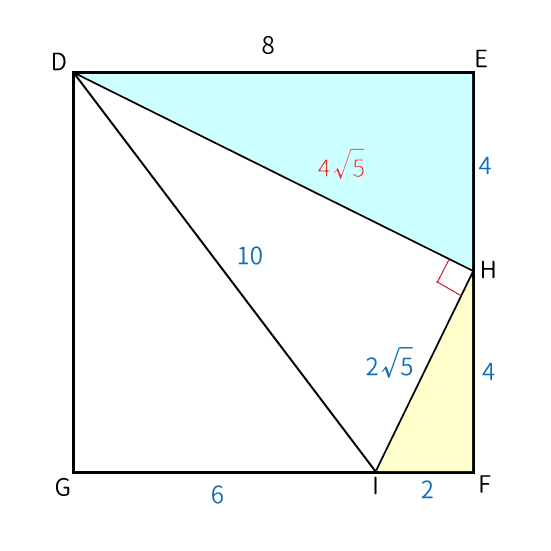
$FI$と$EH$の比は$FI:EH=2:4=1:2$

$HF$と$DE$の比は$HF:DE=4:8=1:2$

$\angle DEH=\angle HFI=90^{\circ}$

上記3点より、直角三角形の相似条件は2組の辺の比が等しければよいので、

$\bigtriangleup DEH$と$\bigtriangleup HFI$は相似である。

$\bigtriangleup DHI$と$\bigtriangleup HFI$は相似？

$FI$と$HI$の比は$FI:HI=2:2\sqrt{5}=1:\sqrt{5}$

$HF$と$DH$の比は$HF:DH=4:4\sqrt{5}=1:\sqrt{5}$

$\angle DHI=\angle HFI=90^{\circ}$

上記3点より、直角三角形の相似条件は2組の辺の比が等しければよいので、

$\bigtriangleup DHI$と$\bigtriangleup HFI$は相似である。

よって、$\bigtriangleup DEH$と$\bigtriangleup DHI$の2つが相似である（選択肢：１）。

$\angle DIG$と$\angle DIH$を比較

$\angle DIG$と$\angle DIH$を比較するために、それぞれの$cos$の値を求める。

$\displaystyle cos \angle DIG = \frac{6}{10}=\frac{3}{5}$

$\displaystyle cos \angle DIH = \frac{2\sqrt{5}}{10}=\frac{\sqrt{5}}{5}$

$\sqrt{5}$は、富士山麓オウム鳴く（ふじさんろくおうむなく）なので、

$\sqrt{5}=2.2360679…$である。

よって、$3>\sqrt{5}$なので、$\displaystyle \frac{3}{5}>\frac{\sqrt{5}}{5}$となり、

$cos \angle DIG > cos \angle DIH $である。

ここで$0\leq \theta < 90$のとき$cos \theta$は$\theta$の値（角度）が大きくなるほど、$cos \theta$の値は小さくなる。

つまり、$cos \theta$の値が小さい方が角度は大きなる。

よって、$cos \angle DIG > cos \angle DIH $なので不等号が反対になり、$\angle DIG < \angle DIH $（選択肢：３）となる。

$0\leq \theta < 90$のときの$cos \theta$の性質について

「$0\leq \theta < 90$のとき$cos \theta$は$\theta$の値（角度）が大きくなるほど、$cos \theta$の値は小さくなる。」

これは単位円から$cos \theta$を見ると簡単に理解できます。

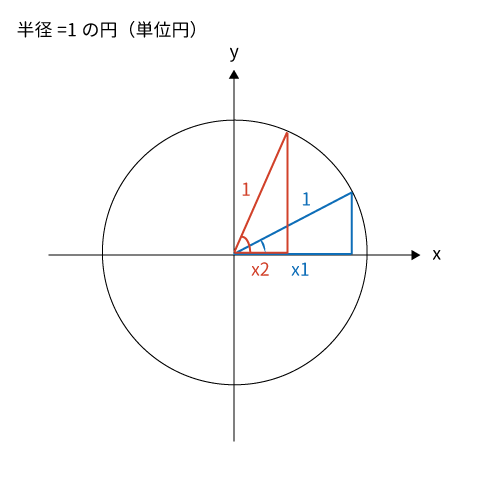
半径が$1$である単位円では$cos \theta$の値は$\displaystyle \frac{x座標}{半径}$です。半径は$1$なので、$cos \theta$の値は$x$座標の値となります。

よって、青い三角の$cos \theta 1=x1$、赤い三角の$cos \theta 2= x2$となります。$x2$より$x1$の方が長く、赤い三角より青い角度の方が小さいのは図より明らかです。つまり、$cos$の値が大きい程、角度は小さくなります。

上の図より、赤よりも角度が$90^{\circ}$に近づけば（角度が大きくなれば）、$x$の値は$0$に近づいていくので、小さくなることが分かります。

反対に角度が$0^{\circ}$に近づけば（角度が小さくなれば）、$x$の値は$1$に近づいていくので、大きくなります。

スポンサーリンク