令和2年センター本試＞数１A＞第2問 [1] 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第２問 [１]

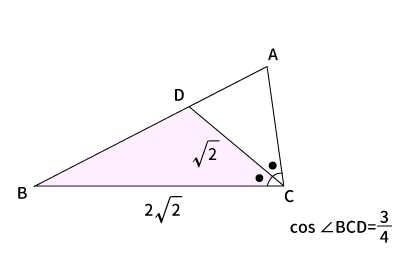
$\bigtriangleup ABC$において、$BC=2\sqrt{2}$ 、$\angle ACB$の二等分線と辺$AB$の交点を$D$とし、$CD=\sqrt{2}$、$\displaystyle \cos \angle BCD = \frac{3}{4}$とするので、上図のようになる。

このとき$BD$は「余弦定理」より、

なので、

$BD=\pm 2$

BDは辺の長さなので正。よって、$BD=2$

$\sin \angle ADC $の値

三角比の相互関係より$\sin \angle BCD$を求める

三角比の相互関係$\sin^2 \theta  + \cos^2 \theta  =1$より、

$\displaystyle \sin \angle BCD =\pm \frac{\sqrt{7}}{4}$

$\angle BCD $は$\bigtriangleup DBC$の内角の1つなので$\angle BCD \leq 90$である。よって、$0 \leq \sin \angle BCD \leq 1$。

従って、$\displaystyle \sin \angle BCD =\frac{\sqrt{7}}{4}$

正弦定理より$\sin \angle CDB $を求める

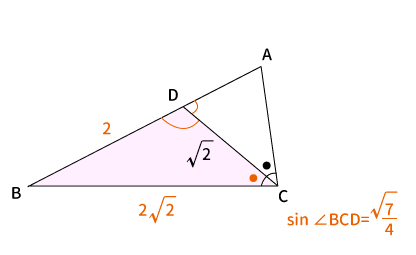
$\bigtriangleup DBC$に対して「正弦定理」より、

$\displaystyle \frac{BD}{\sin \angle BCD} = \frac{BC}{\sin \angle CDB} $

変形すると、

$BD \sin \angle CDB =BC \sin \angle BCD$

各値を代入すると、

$\displaystyle 2 \sin \angle CDB = 2\sqrt{2} \frac{\sqrt{7}}{4}$

$\displaystyle \sin \angle CDB = \frac{\sqrt{14}}{4}$

$\angle ADC = 180^{\circ} – \angle CDB$より$\sin \angle ADC$が求まる

三角比の関係より、$\sin(180^{\circ}-\theta)=\sin \theta$なので、

よって、$\displaystyle \sin \angle ADC= \frac{\sqrt{14}}{4}$

$\displaystyle \frac{AC}{AD}$

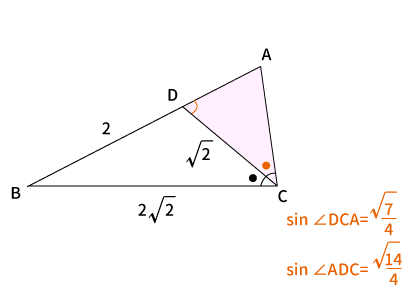
$\angle DCA = \angle BCD$より、$\sin \angle DCA$を求める

$\angle DCA = \angle BCD$より、

$\displaystyle \sin \angle DCA =\sin \angle BCD =\frac{\sqrt{7}}{4}$

よって、$\displaystyle \sin \angle DCA =\frac{\sqrt{7}}{4}$

正弦定理より$\displaystyle \frac{AC}{AD}$を求める

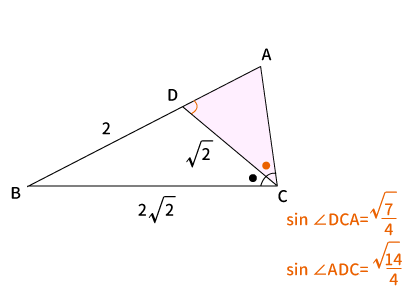
$\bigtriangleup ADC$に対して「正弦定理」より、

$\displaystyle \frac{AC}{\sin \angle ADC} = \frac{AD}{\sin \angle DCA} $

変形すると、

$\displaystyle AC \sin \angle DCA= AD \sin \angle ADC $

$\displaystyle \sin \angle ADC= \frac{\sqrt{14}}{4}$、$\displaystyle \sin \angle DCA =\frac{\sqrt{7}}{4}$を代入すると、

$\displaystyle \frac{\sqrt{7}}{4}AC= \frac{\sqrt{14}}{4} AD $

$\displaystyle \frac{AC}{AD}= \sqrt{2}  $

$AD$の値

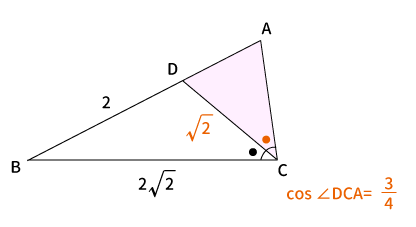
$\bigtriangleup ADC$に対して「余弦定理」より、

各値を代入すると、

$\displaystyle AD^2 = \sqrt{2}^2 + CA^2 – 2 \times \sqrt{2} \times CA \times \frac{3}{4}$

また、先ほどの答え$\displaystyle \frac{AC}{AD}= \sqrt{2}  $より、$AC=\sqrt{2}AD$である。こちらも代入すると、

$0 = (AD-1)(AD-2)$

よって、$AD$は$1$または$2$である。

ここで$AD=2$の場合を考える

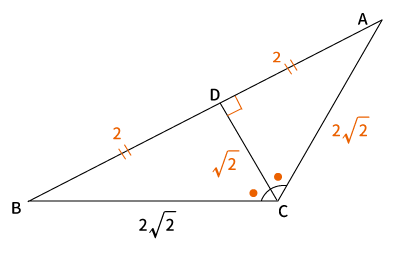
$\displaystyle \frac{AC}{AD}= \sqrt{2}  $、$AD=2$より、$AC=2\sqrt{2}$

この場合、上図を見てわかる通り$\bigtriangleup ABC$は2等辺三角形となり、$DC$は$C$から$AB$への垂線となる。よって、$\angle ADC = 90^{\circ}$となる。つまり$\bigtriangleup ADC$は直角三角形である。

$\bigtriangleup ADC$は直角三角形なので三平方の定理より$AD^2+DC^2=CA^2$を満たすはずです。

ですが、値を代入して$2^2+\sqrt{2}^2=(2\sqrt{2})^2$、計算すると$4+2=8$。三平方の定理を満たしませんでした。

よって、$AD=2$は正しくありません。

ゆえに$AD=1$

$\bigtriangleup ABC$の外接円の半径

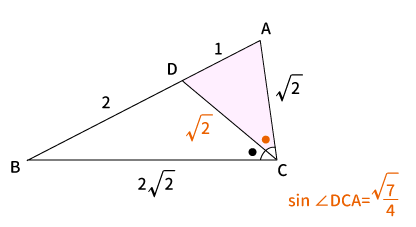
$\bigtriangleup ADC$に対して「正弦定理」より、

$\displaystyle \frac{AD}{\sin \angle DCA} = \frac{DC}{\sin \angle CAD} $

変形すると、

$\displaystyle AD \sin \angle CAD= DC \sin \angle DCA $

各値を代入すると、

$\displaystyle \sin \angle CAD= \sqrt{2}\frac{\sqrt{7}}{4} =\frac{\sqrt{14}}{4}$

正弦定理より$\bigtriangleup ABC$の外接円の半径を求める

$\bigtriangleup ABC$に対して「正弦定理」より、$R$を外接円の半径とすると

$\displaystyle 2R = \frac{BC}{\sin \angle CAD}$

各値を代入すると、

$\displaystyle 2R = \frac{2\sqrt{2}}{\frac{\sqrt{14}}{4}}$

$\displaystyle R =\frac{4\sqrt{7}}{7}$

よって、$\bigtriangleup ABC$の外接円の半径は$\displaystyle \frac{4\sqrt{7}}{7}$

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

三角比、2等分線、余弦定理、正弦定理、外接円、三平方の定理