令和2年センター本試＞数２Ｂ＞第2問 (3)解いてみた

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第２問 （３）

前回より、分かっていることは、

• 放物線$C$：$y=x^2+2x+1$
• 放物線$D$：$y=x^2-(4a-2)x+4a^2+1$
• 直線$l$：$y=2x+1$
• $C$と直線$l$、および直線$x=a$で囲まれた図形の面積$S$：$\displaystyle S=\frac{a^3}{3}$

2つの放物線$C$、$D$と直線$l$で囲まれた図形の中で$0 \leq x\leq 1$を満たす部分の面積を$T$とする。

面積$T$が$a$の値によらないのは？

2つの放物線$C$、$D$と直線$l$で囲まれた図形は下図の「オレンジ＋青」部分になる。その内$0 \leq x\leq 1$を満たす部分が面積$T$となるので、オレンジ部分が面積$T$である。

ここで分かるのは、$a>1$の場合、$a$がどれだけ大きくなっても上図青部分だけが大きくなるだけで面積$T$は変わらない。その理由は$C$、$D$の交点が$x=1$より大きくなると、$D$の放物線の影響を受けなくなるためである。
※下の図を見ると少しイメージできるかと思います

次に$a\leq1$の場合は下のようになる。$\displaystyle \frac{1}{2} < a$という条件があるので、$\displaystyle a=\frac{1}{2} $の場合にしている。

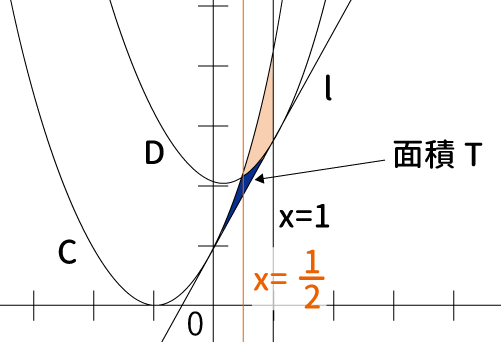
$\displaystyle a=\frac{1}{2} $の場合の面積$T$が青部分、$a=1 $の場合はオレンジ部分も含めたものである。つまり、$\displaystyle \frac{1}{2} < a \leq1$の場合は、$a$の値によって、面積$T$の大きさが変わる。

以上より、$a > 1$のとき面積$T$は$a$に依存しない。

$a > 1$のとき面積$T$は？

$a > 1$のときは前回の「$C$と直線$l$、および直線$x=a$で囲まれた図形の面積$S$：$\displaystyle S=\frac{a^3}{3}$」が使える。

図からも分かるように、$a=1$を代入すれば、面積$T$は求まるので、

$\displaystyle T=\frac{1^3}{3}=\frac{1}{3}$

$\displaystyle \frac{1}{2} < a \leq 1$のとき面積$T$は？

先ほどの上図から分かるとおり、$\displaystyle \frac{1}{2} < a \leq 1$の面積$T$は$x=a$で分断した2つの面積を足せばよいのが分かる（下図「青＋赤」）。

青の面積

青の方は、先ほどと同様で前回の「$C$と直線$l$、および直線$x=a$で囲まれた図形の面積$S$：$\displaystyle S=\frac{a^3}{3}$」が使える。$a$のままで良いので、青の面積は$\displaystyle \frac{a^3}{3}$である。

赤の面積

赤の面積は「$D$と直線$l$、および直線$x=a$で囲まれた図形の面積」である。よって、前回と同じように定積分で面積を求めることができる。図から分かる通り定積分の範囲は$a$～$1$である。

$D$が$y=x^2-(4a-2)x+4a^2+1$、直線$l$が$y=2x+1$なので、$D$の方の定積分から直線$l$の定積分を引けばよいので、

赤部分の面積は$\displaystyle -\frac{7}{3}a^3+4a^2-2a+\frac{1}{3}$である。

よって、面積$T$は、$\displaystyle \frac{a^3}{3}$と$\displaystyle -\frac{7}{3}a^3+4a^2-2a+\frac{1}{3}$を足したものなので
$\displaystyle \frac{a^3}{3} -\frac{7}{3}a^3+4a^2-2a+\frac{1}{3}$

従って、$\displaystyle  T = -2a^3+4a^2-2a+\frac{1}{3}$

スポンサーリンク