![令和2年センター本試>数1A>第3問 [2] 解いてみた](https://math.lucklog.info/wp/wp-content/uploads/2021/06/center.png)
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
問題
問題は下記を開いてご確認ください。
第3問 [2]
(1) コインを2回投げ終わって持ち点が$-2$点である確率
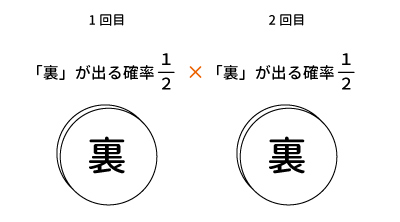
コインを2回投げ終わって持ち点が$-2$になるのは「裏」「裏」が出た場合のみである。
1回目、2回目ともに「裏」で出る確率は$\displaystyle \frac{1}{2}$なので、コインを2回投げ終わって持ち点が$-2$点である確率は$\displaystyle (\frac{1}{2})^2 =$$\displaystyle \frac{1}{4}$
(1) コインを2回投げ終わって持ち点が$1$点である確率
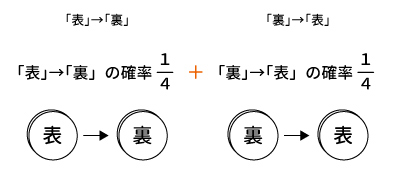
コインを2回投げ終わって持ち点が$1$になるのは「表」「裏」の組み合わせだった場合である。つまり、「表→裏」「裏→表」の2通り。
1回目、2回目ともに「表」「裏」どちらの場合も出る確率は$\displaystyle \frac{1}{2}$なので、「表→裏」「裏→表」どちらのパターンでもそれぞれ起こる確率は$\displaystyle (\frac{1}{2})^2 =\frac{1}{4}$
「表→裏」「裏→表」のどちらが起きても持ち点は$1$点なので、これらの確率を足しあわせれば良い。(パターン分同じ確率を足すので確率にパターン数を掛ければ良い)
よって、コインを2回投げ終わって持ち点が$1$点である確率は$\displaystyle \frac{1}{4} \times 2 = $$\displaystyle \frac{1}{2}$
(2) 持ち点が再び$0$点になることが起きるのは何回投げ終わったとき?
「表」だと$2$点、「裏」だと$-1$点なので、$0$点になるには「表」:「裏」が$1:2$の比率になる必要がある。つまり、「表」が1回であれば、「裏」は2回。「表」が2回であれば、「裏」は4回必要である。
しかし、「表」が2回で「裏」が4回の場合は合計6回投げる必要があり、最大5回を超えてしまっている。
よって、持ち点が再び$0$点になることが起きるのは「表」が1回で「裏」が2回の場合、つまりコインを3回投げ終わったときのみである。
(2) コインを3回投げ終わって持ち点が$0$点になる確率は?
コインを3回投げ終わって持ち点が$0$になるのは「表」が1回で「裏」が2回の場合である。つまり、「表」「裏」「裏」の組み合わせの場合なので、$\displaystyle _3C_1=\frac{3}{1}=3$通りである。
「表」「裏」「裏」の組み合わせを次のように考えます。
A、B、Cという3つの机があって、そこに1枚ずつ置くとします。どのような置くか考えるとき、「表」を置く机をA、B、Cの中から1つ選ぶと考えます。「裏」は残った机に置くだけなので何も考えなくてOKです。つまり、「表」を置く机をA、B、Cの中から1つ選ぶだけで、「表」「裏」「裏」の置き方が何通りあるか分かるのです。
「3つの中から1つを選ぶ」これは、組み合わせの公式が使えますね。よって、$_3C_1$となります。
ちなみに「裏」を置く机をA、B、Cの中から2つ選ぶと考えても問題ありません。その場合$\displaystyle _3C_2=\frac{3・2}{2}=3$通り。同じになります。
3通りそれぞれが起こる確率は、(1) と同様に1回目、2回目、3回目ともに「表」「裏」どちらが出る確率も$\displaystyle \frac{1}{2}$なので、$\displaystyle (\frac{1}{2})^3 =\frac{1}{8}$
「表」「裏」「裏」の組み合わせのどれが起きても持ち点は$0$点なので、これらの確率を足しあわせれば良い。(パターン分同じ確率を足すので確率にパターン数を掛ければ良い)
よって、コインを3回投げ終わって持ち点が$0$点になる確率は$\displaystyle \frac{1}{8} \times 3 = $$\displaystyle \frac{3}{8}$
(3) ゲームが終了した時点で持ち点が$4$点ある確率
持ち点が$4$点になるには、「表」「表」または「表」「表」「表」「裏」「裏」の組み合わせが必要である。しかし、「表」「表」の組み合わせでゲームを終えることはできないので、「表」「表」「表」「裏」「裏」の組み合わせの場合のみである。
また、最初の3回の組み合わせが「表」「裏」「裏」の場合、持ち点が$0$点になり3回目でゲーム終了となるので、考えられる最初の組み合わせは「表」「表」「表」、「表」「表」「裏」のどちらかの組み合わせである。
最初の3つの組み合わせが「表」「表」「表」の場合
最初の3つの組み合わせが「表」「表」「表」の場合は、「表」「表」「表」「裏」「裏」の1通り。
最初の3つの組み合わせが「表」「表」「裏」の場合
最初の3つの組み合わせが「表」「表」「裏」の場合は、$_3C_2=3$通りである。また3通りに対して残りの「表」「裏」の組み合わせが考えられる。「表」「裏」の組み合わせは$_2C_1=2$なので、「表」「表」「裏」の組み合わせで始まるのは$3\times2=6$通り。

よって、ゲームが終了した時点で持ち点が$4$点あるのは計7通りである。
7通りがそれぞれ起こる確率
ゲーム終了時に持ち点が$4$点になるのは「表」「表」「表」「裏」「裏」の組み合わせ、つまりコインを5回投げ終わったときのみである。
よって、1~5回目まですべて「表」「裏」の$\displaystyle \frac{1}{2}$なので、7通りそれぞれが起こる確率はすべて$\displaystyle (\frac{1}{2})^5=\frac{1}{32}$である。
従って、ゲームが終了した時点で持ち点が$4$点ある確率はこれら7つの確率を足した$\displaystyle \frac{1}{32} \times 7=$$\displaystyle \frac{7}{32}$となる。
(4) ゲームが終了した時点で持ち点が$4$点であるとき、コインを2回投げ終わって持ち点が$1$点である条件付き確率
条件付き確率とあるが、普通の確率と同じように考える。つまり、全体が分母、聞かれている確率が分子で考えればよい。
今回の場合、分母(全体)はゲームが終了した時点で持ち点が$4$点の確率、分子はゲームが終了した時点で持ち点が$4$点でかつ、コインを2回投げ終わったときは持ち点が$1$点だった確率である。
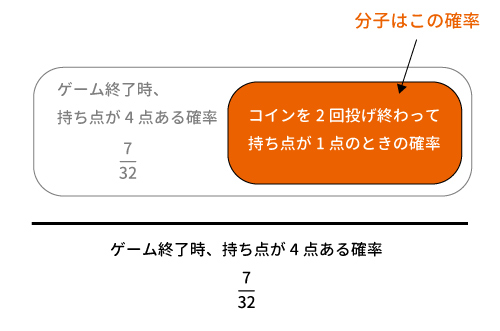
ゲームが終了した時点で持ち点が$4$点ある確率は$\displaystyle \frac{7}{32}$と分かっているので、ゲームが終了した時点で持ち点が$4$点でかつ、コインを$2$回投げ終わったときは持ち点が$1$点だった確率を求める。
ゲームが終了した時点で持ち点が$4$点でかつ、コインを2回投げ終わったときは持ち点が$1$点だった確率
(1) の回答でコインを2回投げ終わって持ち点が$1$点である確率は$\displaystyle \frac{1}{2}$と分かっているので、3回目以降を考える。また、(1) の回答で2回投げ終わった時点で「表」「裏」が1回ずつ出ていることも分かっている。
3回目に「裏」がでると持ち点が$0$点になりゲーム終了してしまうので、3回目は「表」しかない。つまり3回目が終了時点で「表」2回「裏」1回である。
4回目、5回目は?
(3) よりゲームが終了した時点で持ち点が$4$点である組み合わせは「表」「表」「表」「裏」「裏」と分かっている。3回目が終了時点で「表」2回「裏」1回は既に出ているので、4回目、5回目は「表」「裏」の組み合わせになり、$_2C_1=2$通りと分かる。
整理すると
これまでに分かったことを整理する。
- 2回目までの確率が$\displaystyle \frac{1}{2}$
- 3回目以降のパターンは$2$通り
よって、3回目以降の2通りがそれぞれ起こる確率は、2回目までの確率$\displaystyle \frac{1}{2}$に対して、3回目以降がそれぞれ「表」「裏」の$\displaystyle (\frac{1}{2})^3$なので、
$\displaystyle \frac{1}{2} \times (\frac{1}{2})^3=(\frac{1}{2})^4$
そして、この確率が2通りあるので、ゲームが終了した時点で持ち点が$4$点でかつ、コインを2回投げ終わったときは持ち点が$1$点だった確率は$\displaystyle (\frac{1}{2})^4 \times 2=(\frac{1}{2})^3$である。
以上より、必要な情報は揃ったので、下記を計算すると、
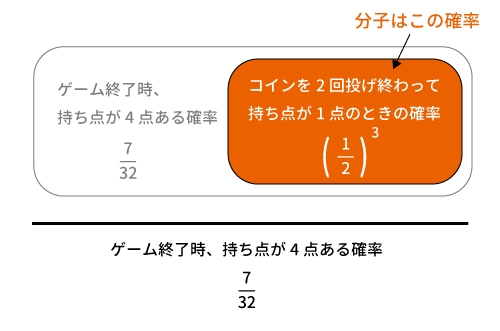
$\displaystyle (\frac{1}{2})^3 \div \frac{7}{32}$
$\displaystyle (\frac{1}{2})^3 \div \frac{7}{32} = (\frac{1}{2})^3 \times \frac{32}{7}$
$\displaystyle =\frac{1}{2^3} \times \frac{2^5}{7}$
$\displaystyle =\frac{2^2}{7}$
$\displaystyle =\frac{4}{7}$
よって、ゲームが終了した時点で持ち点が$4$点であるとき、コインを2回投げ終わって持ち点が$1$点である条件付き確率は$\displaystyle \frac{4}{7}$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています