
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
問題
問題は下記を開いてご確認ください。
第4問 (2)
- 点$O$を原点とする座標空間に2点$A(3, \, 3, \, -6)$、$B(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$をとる
- 3点$O$、$A$、$B$の定める平面を$\alpha$とする
- $\alpha$に含まれる点$C$は$\overrightarrow{OA} \perp \overrightarrow{OC}$、$\overrightarrow{OB} \cdot \overrightarrow{OC}=24$・・・( i )を満たす
- $\overrightarrow{OA} \cdot \overrightarrow{OB} = 36$
実数$s$、$t$を用いて、$\overrightarrow{OC} = s \, \overrightarrow{OA} + t \, \overrightarrow{OB}$と表せる。
$s$、$t$の値は?
( i ) $\overrightarrow{OA} \perp \overrightarrow{OC}$より、内積は$0$なので$\overrightarrow{OA} \cdot \overrightarrow{OC}=0$
$\overrightarrow{OC} = s \, \overrightarrow{OA} + t \, \overrightarrow{OB}$を代入すると、
$\overrightarrow{OA} \cdot (s \, \overrightarrow{OA} + t \, \overrightarrow{OB})=0$
$\overrightarrow{OA} \cdot (s \, \overrightarrow{OA} + t \, \overrightarrow{OB})=0$
$s \, \overrightarrow{OA} \cdot \overrightarrow{OA} + t \, (\overrightarrow{OA} \cdot \overrightarrow{OB})=0$
$\overrightarrow{OA} \cdot \overrightarrow{OB}=36$なので、
$s \, (9+9+36) + 36t =0$
$54s + 36t =0$
$3s + 2t =0$
$3s + 2t =0$・・・ ( ii )
$3s + 2t =0$・・・ ( ii )
( i ) $\overrightarrow{OB} \cdot \overrightarrow{OC}=24$に、$\overrightarrow{OC} = s \, \overrightarrow{OA} + t \, \overrightarrow{OB}$を代入すると、
$\overrightarrow{OB} \cdot (s \, \overrightarrow{OA} + t \, \overrightarrow{OB})=24$
$\overrightarrow{OB} \cdot (s \, \overrightarrow{OA} + t \, \overrightarrow{OB})=24$
$s \, \overrightarrow{OB} \cdot \overrightarrow{OA} + t \, \overrightarrow{OB} \cdot \overrightarrow{OB}=24$
内積は交換可能なので、
$s \, \overrightarrow{OA} \cdot \overrightarrow{OB} + t \, \{ (2+2\sqrt{3})^2 + (2-2\sqrt{3})^2 + 16 \})=24$
$s \, \overrightarrow{OA} \cdot \overrightarrow{OB} + t \, \{ 4+12+4+12+16 \})=24$
$\overrightarrow{OA} \cdot \overrightarrow{OB}=36$なので、
$36s + 48t =24$
$3s + 4t =2$
$3s + 4t =2$・・・ ( iii )
$3s + 4t =2$・・・ ( iii )
( iii ) $3s + 4t =2$から( ii ) $3s + 2t =0$ を引くと、
$2t = 2$ 、ゆえに$t = 1$
$t=1$を( ii ) $3s + 2t =0$に代入すると、
$3s + 2 =0$、ゆえに$\displaystyle s=-\frac{2}{3}$
$| \overrightarrow{OC} |$の値は?
$\overrightarrow{OC} = s \, \overrightarrow{OA} + t \, \overrightarrow{OB}$に$A(3, \, 3, \, -6)$、$B(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$、$t = 1$、$\displaystyle s=-\frac{2}{3}$を代入すると、
$\displaystyle \overrightarrow{OC} = -\frac{2}{3} \, (3, \, 3, \, -6) + (2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$
$\displaystyle \overrightarrow{OC} = -\frac{2}{3} \, (3, \, 3, \, -6) + (2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$
$\displaystyle \overrightarrow{OC} = (-2, \, -2, \, 4) + (2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$
$\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$
$\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$
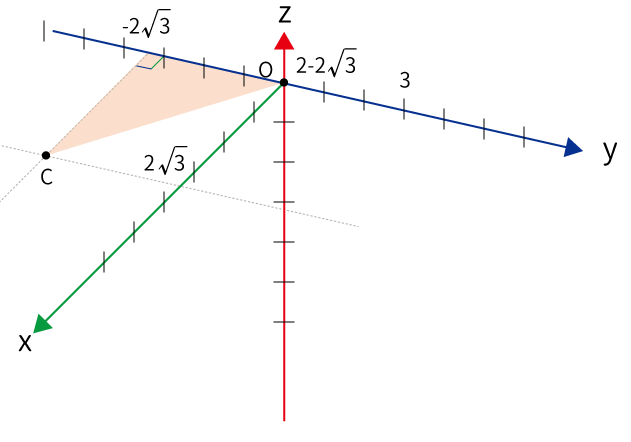
$\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$、三平方の定理より、
$|\overrightarrow{OC}|^2 = (2\sqrt{3})^2 + (-2\sqrt{3})^2$
$|\overrightarrow{OC}|^2 = (2\sqrt{3})^2 + (-2\sqrt{3})^2$
$= 12+ 12 = 24$
$|\overrightarrow{OC}|^2 = 24$
よって、$|\overrightarrow{OC}| = \sqrt{24}=$$2\sqrt{6}$
※絶対値なので正のみ
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています