正しく証明・計算の結果が学術的に本当に正しいかどうかは保証できません…ご了承くださいm(__)m
学生の方であれば、疑問に思ったところなどは教授・助教授、その他周りの方に確認してくださいね。
もし、コメント等でご指摘いただければ有難いです。
要素$a$、$b$に対して対の公理が主張する集合は一意に決まる
「{x, y}が一意に定まることを証明せよ」にて、要素$a$、$b$に対して対の公理が主張する集合は一意に決まることが分かっているので、その集合を$\{a, b\}$と書くことにします。
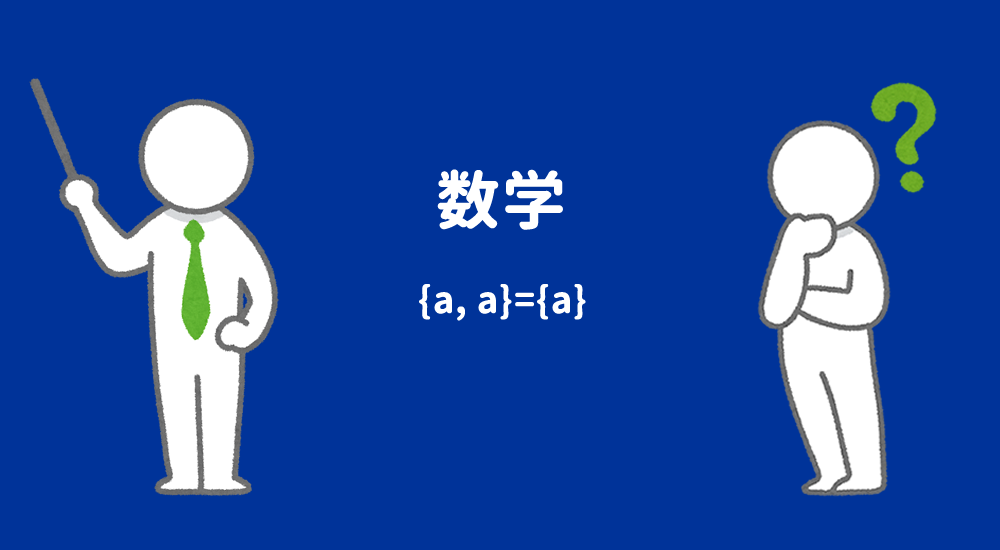
ここで、$a=b$の場合も同様に一意に定まるので、この集合を$\{a, a\}$と書きますが、これは元aのみを持つ集合なので、$\{a\}$と書くことにします。また1つの元からなる集合を一元集合と呼びます。
キーワード
気になる人は調べてみてね。
公理的集合論、対の公理、一元集合、論理式、全称記号($\forall$)、 等号(=)、含意($\to$)、同値($\leftrightarrow$)、Q.E.D.
正しく証明・計算の結果が学術的に本当に正しいかどうかは保証できません…ご了承くださいm(__)m
学生の方であれば、疑問に思ったところなどは教授・助教授、その他周りの方に確認してくださいね。
もし、コメント等でご指摘いただければ有難いです。



