
三角関数の加法定理の$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$を証明してみたいと思います。これ以外の加法定理は$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$を元に求められますので、別記事にしたいと思います。
求められる加法定理
$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
$\cos(\alpha-\beta)$$=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
まずはざっくりとした流れを説明します。
ざっくりとした流れ
単位円の円周上に2点取り、角度が大きい方($\alpha$)から小さい方($\beta$)を引きます。すると、$\alpha-\beta$という形ができます。
次に、半径が$1$ということから、余弦定理と三角比の相互関係、$\cos^2 \theta + \sin^2 \theta=1$および三平方の定理から$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$を導くことができます。
それでは詳細を見ていきます。
$\beta-\alpha$
$\alpha$
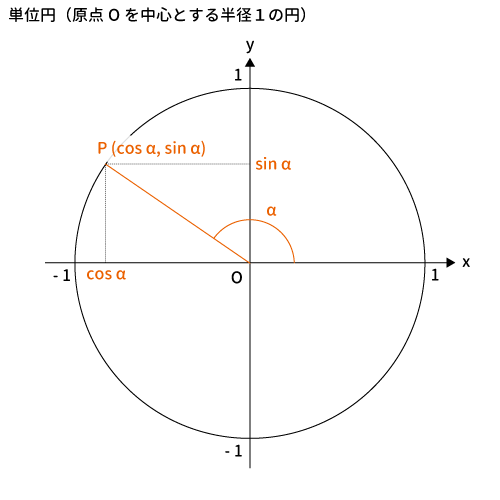
まずは単位円の円周上に点$P$をとり、その角度を$\alpha$と置きます。
$P$の座標は$(\cos\alpha, \, \sin\alpha)$です。
※$x$座標は$\cos$、$y$座標は$\sin$となります。詳細は「単位円とは?」をご覧ください
$\beta$
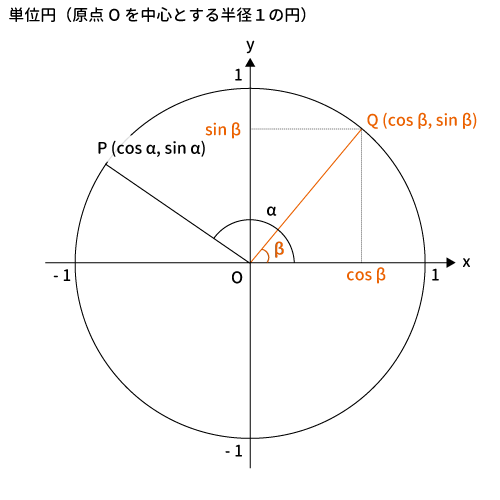
同様に単位円の円周上に点$Q$をとり、その角度を$\beta$と置きます。
$Q$の座標は$(\cos\beta, \, \sin\beta)$です。
※$x$座標は$\cos$、$y$座標は$\sin$となります。詳細は「単位円とは?」をご覧ください
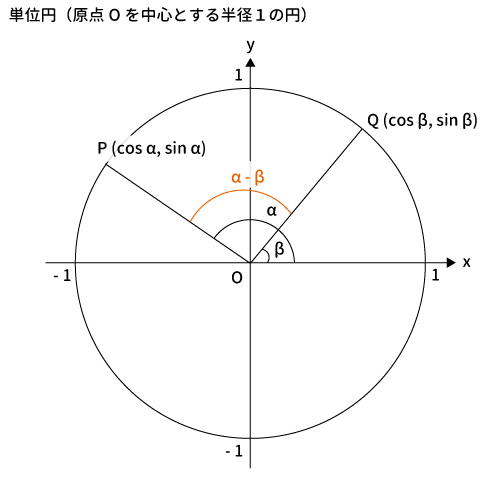
よって、下記オレンジ部分が$\alpha-\beta$となります。
余弦の定理より
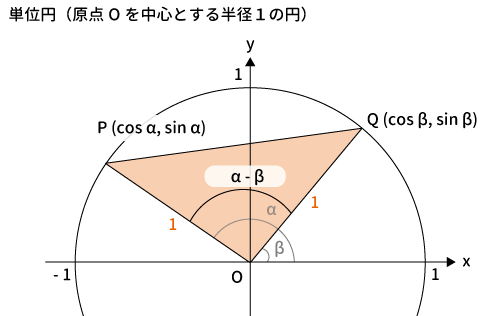
$\bigtriangleup OPQ$に対して余弦の定理より、下記が成り立ちます。
$PQ^2=OP^2+OQ^2-2・OP・OQ・\cos(\alpha-\beta)$
また、単位円より半径は$1$なので、$OP=1$、$OQ=1$となり、
$PQ^2=1+1-2・1・1・\cos(\alpha-\beta)$
$\color{white}PQ^2\color{black}=2-2\cos(\alpha-\beta)$
求めたい値は$\cos(\alpha-\beta)$なので、上の式を少し変形します。
$PQ^2=2-2\cos(\alpha-\beta)$
$2\cos(\alpha-\beta)=2-PQ^2$
$\displaystyle \cos(\alpha-\beta)=\frac{2-PQ^2}{2}$
変形した$\displaystyle \cos(\alpha-\beta)=\frac{2-PQ^2}{2}$の式を( i ) と置きます。
後は$PQ^2$が分かれば$\cos(\alpha-\beta)$が求まります。
$PQ^2$を求める
$P$を通る$y$軸と平行な線と、$Q$を通る$x$軸と平行な線との交点を$S$とします。$S$の座標は、$x$座標は$P$と同じ、$y$座標は$Q$と同じなので、$S(\cos\alpha, \, \sin\beta)$となります。
ここでできた$\bigtriangleup PQS$から$PQ^2$を求めます。
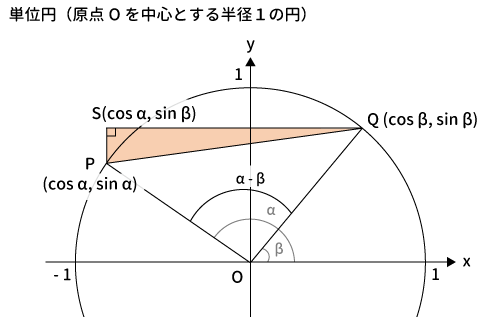
三角形の辺の長さ
$P$、$Q$、$S$の座標から各長さは絶対値を用いて下記のとおりです。
$QS$は$\cos \beta$と$-\cos\alpha$を足したもの、$PS$は$\sin \beta$と$\sin\alpha$を引いたものが長さになります。
$S$から$y$軸までの長さが$-\cos\alpha$のようにマイナスが付いています。その理由は、$\cos\alpha$はマイナス座標にあり負の値なので正にするためにマイナスをつけています。
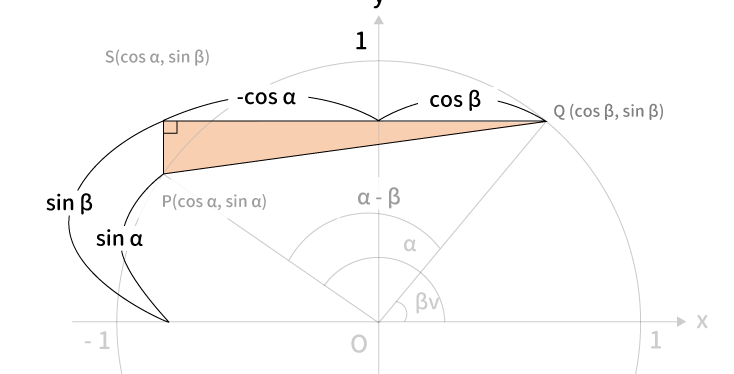
よって、$PS=\cos \beta-\cos \alpha$、$QS=\sin\beta-\sin\alpha$となります。
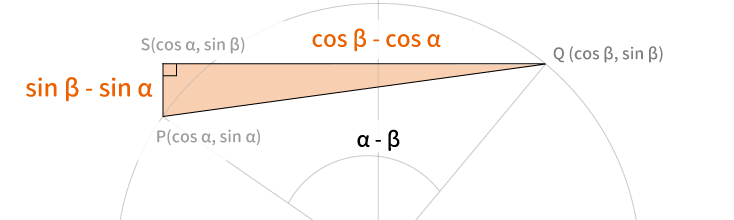
三平方の定理より
$\bigtriangleup PQS$は直角三角形なので、
$PQ^2=PS^2+QS^2$となり、$PS=\cos \beta-\cos \alpha$と$QS=\sin\beta-\sin\alpha$を代入すると、
$PQ^2=PS^2+QS^2$
$\color{white}PQ^2\color{black}=(\cos \beta-\cos \alpha)^2 + (\sin\beta-\sin\alpha)^2$
$PQ^2=(\cos \beta-\cos \alpha)^2 + (\sin\beta-\sin\alpha)^2$
$=\cos ^2\alpha-2\cos \alpha\cos \beta+\cos ^2\beta + \sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta$
$=(\sin^2\alpha+\cos ^2\alpha)+(\sin^2\beta+\cos ^2\beta)- 2\cos \alpha\cos \beta -2\sin\alpha\sin\beta$
ここで、$sin^2\theta+\cos ^2\theta=1$なので、
$=1+1- 2\cos \alpha\cos \beta -2\sin\alpha\sin\beta$
$=2- 2\cos \alpha\cos \beta -2\sin\alpha\sin\beta$
$PQ^2=2-2\cos \alpha\cos \beta -2\sin\alpha\sin\beta$
結果
( i ) $\displaystyle \cos(\alpha-\beta)=\frac{2-PQ^2}{2}$に$PQ^2=2-2\cos \alpha\cos \beta -2\sin\alpha\sin\beta$を代入します。
$\displaystyle \cos(\alpha-\beta)=\frac{2-(2-2\cos \alpha\cos \beta -2\sin\alpha\sin\beta)}{2}$
$\displaystyle \cos(\alpha-\beta)=\frac{2-2+ 2\cos \alpha\cos \beta +2\sin\alpha\sin\beta}{2}$
$\displaystyle \cos(\alpha-\beta)=\cos \alpha\cos \beta +\sin\alpha\sin\beta$
$\displaystyle \cos(\alpha-\beta)=\cos \alpha\cos \beta +\sin\alpha\sin\beta$
以上より、加法定理の$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$を導くことができました。
証明終了です。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
加法定理、三角関数、単位円、三角比の相互関係、余弦の定理、三平方の定理、$\sin \theta$、$\cos \theta$



