令和2年センター本試＞数１＞第2問 [2] 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第２問 [2]（１）

第２問 [1]（１）（別解）より、$y=x^2+ax+b$は、$(\displaystyle \frac{-a – \sqrt{a^2 -4b } }{2}, \, 0)$と$(\displaystyle \frac{-a + \sqrt{a^2 -4b } }{2}, \, 0)$の2点を通ることが分かっている。

グラフGは2点$(c, \, 0)$、$(c+4, \, 0)$を通るので、以下2つの式から、$a$と$b$の値を$c$を用いて表せれば、二次関数を$c$を用いて表せれる。

$\displaystyle c=\frac{-a – \sqrt{a^2 -4b } }{2}$・・・（ i ）

$\displaystyle c+4=\frac{-a + \sqrt{a^2 -4b } }{2}$・・・（ ii ）

$a$を求める

( i )$+$( ii )より、$\sqrt{\, \,}$が打ち消しあうので、$a$が求まる。

$\mathbf{a =-2c-4}$

$b$を求める

$\displaystyle a =-2c-4$を( i )に代入して、$b$を求める。

$\displaystyle c=\frac{-(-2c-4) – \sqrt{(-2c-4)^2 -4b } }{2}$

$\mathbf{b=c^2 + 4c }$

$a$と$b$を代入する

$y=x^2+ax+b$に$a =-2c-4$、$b=c^2 + 4c $を代入すると、

$y=x^2+(-2c-4)x+(c^2 + 4c)$

$y=x^2-2(c+2)x+c(c + 4)$

$G$が点$(3, \, k)$を通るとき

$G$が点$(3, \, k)$を通るので、

$k=3^2-2(c+2)\times3+c(c + 4)$

$k=(c-1)^2-4$

$k$の取りうる最小値

$k$は$k=(c-1)^2-4$なので、最小値は正の値である$(c-1)^2$が$0$になったときである。

よって、$k=-4$が最小値である。

$-3 \geq k \geq 0$であるような$c$の値の範囲

まず、$k=-4$が最小値である。あとは、$(c-1)$の値が大きくなるほど$k$の値は大きくなる。

$(c-1)$の値が大きくなるのは、$c$がどんどん小さくなるか、大きくなるかのどちらかである。$k=-3$になる場合も$c$が小さくなった数と大きくなった数があり、$k=0$の場合も同様がある。よって、それぞれ2パターンずつ範囲を調べる。

$k=-3$の場合

$-3=(c-1)^2-4$

2乗すると$1$になるのは$-1$、$1$なので、

$c-1=1$より、$c=2$・・・( i )
$c-1=-1$より、$c=0$・・・( ii )

$k=0$の場合

$0=(c-1)^2-4$

2乗すると$4$になるのは$-2$、$2$なので、

$c-1=2$より、$c=3$・・・( iii )
$c-1=-2$より、$c=-1$・・・( iv )

$c$の値の範囲

( i )( iii )より、$2 \leq c \leq 3$、( ii )( iv)より、$-1 \leq c \leq 0$

第２問 [2]（２）

上記[2]の（１）より、$G$をグラフにもつ2次関数は$y=x^2-2(c+2)x+c(c + 4)$と書ける。

$y=x^2$がどれだけ平行移動したものか知りたいので、$y=x^2-2(c+2)x+c(c + 4)$の頂点を考える。
※$y=x^2$の頂点は$(0, \, 0)$

$c$の値を求める

上記[2]の（１）より、Gが$(3, \, k)$を通るとき、$k=(c-1)^2-4$と書ける。

$G$は$(3,\, -1)$を通るので、$k=-1$である。

$-1=(c-1)^2-4$

$c=\sqrt{3} + 1$・・・( i )

頂点の座標

第２問 [1]（２）より、$y=x^2+ax+b$の頂点は$\displaystyle (- \frac{a}{2},  \, -\frac{a^2}{4}+b)$である。

$G$の場合は$y=x^2-2(c+2)x+c(c + 4)$なので、$a=-2(c+2)=-2c-4$、$b=c(c + 4)=c^2+4c$となり、

頂点は、$\displaystyle (- \frac{-2c-4}{2},  \, -\frac{\{-2c-4\}^2}{4}+c^2+4c)$である。

頂点の$x$座標を求める

$\displaystyle x=- \frac{-2c-4}{2}$

頂点の$x$座標は$ \sqrt{3} + 3$

頂点の$y$座標を求める

$\displaystyle y=-\frac{(-2c-4)^2}{4}+c^2+4c$

頂点の$y$座標は$4$

上記より、頂点の座標は$ (\sqrt{3} + 3, \, -4)$である。

よって、$y=x^2$の頂点$(0, \, 0)$から$x$軸方向に$\sqrt{3} + 3$、$y$軸方向に$-4$平行移動したものであることが分かった。

このときの$y$軸との交点の$y$座標

$x$軸方向に$\sqrt{3} + 3$平行移動しているので、平行移動前の$y=x^2$の値は$x=-(\sqrt{3} + 3)$のときの値である。更に、y軸方向に$-4$平行移動しているので、$x=-(\sqrt{3} + 3)$のときの値から$y$軸方向に$-4$ずれたところが、$y$軸との交点の$y$座標になる。

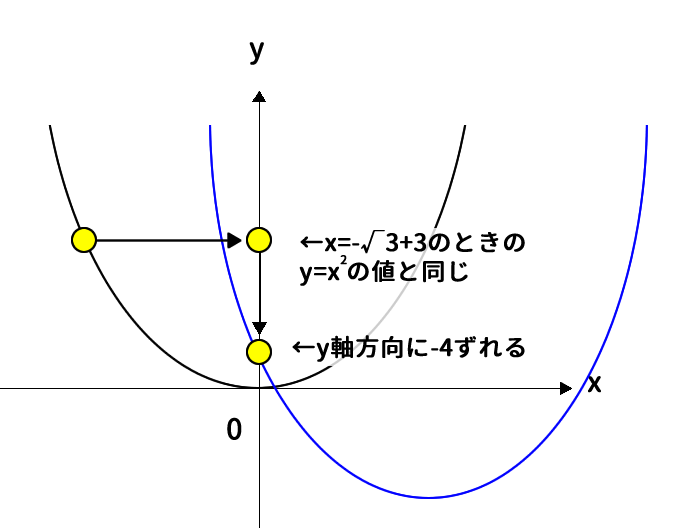
よって、$(-(\sqrt{3} + 3))^2-4$を求めればよい。

よって、このときの$y$軸との交点の$y$座標は$8+6\sqrt{3}$である。

スポンサーリンク