正しく証明・計算の結果が学術的に本当に正しいかどうかは保証できません…ご了承くださいm(__)m
学生の方であれば、疑問に思ったところなどは教授・助教授、その他周りの方に確認してくださいね。
もし、コメント等でご指摘いただければ有難いです。
空集合だけを要素に持つ集合
前回、空集合の発見にて、$\emptyset$(空集合)という集合の存在が確認できました。
それでは次に、対の公理が主張する集合について見ていきます。
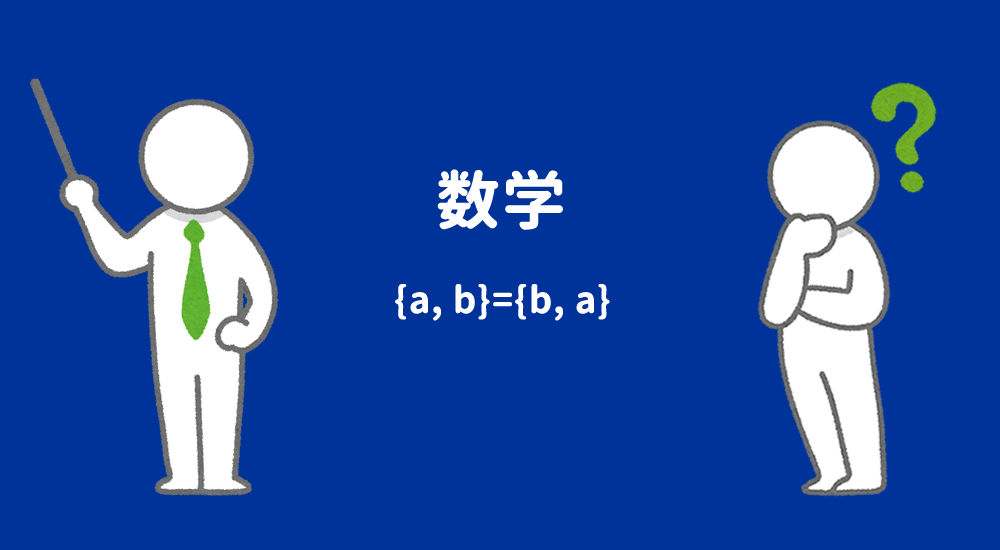
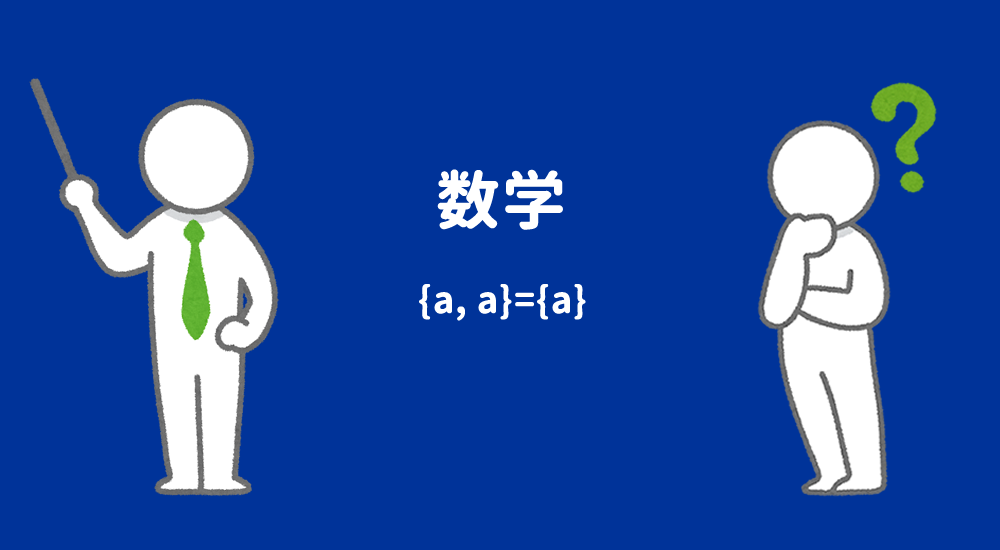
「$x$と$y$という要素に対して、対の公理が主張する集合」は外延性の公理によって、一意に定まることが証明できるので、「$x$と$y$という要素に対して、対の公理が主張する集合」は1つしか存在しません。よって、その集合を$\{x, y\}$と書くことにします。また、$x=y$のとき$\{x\}$と書くことにします。
$\forall x \, \forall y \, \exists A \, \forall t \, (t \notin A \leftrightarrow (t=x \lor t=y))$(任意の要素 x, y に対して、x と y のみを要素とする集合が存在する)
$\forall A \, \forall B \, (\forall x(x \in A \leftrightarrow x \in B) \to A = B)$(任意の集合A、Bが全く同じ要素を持つならば、AとBは等しい)
前回、$\emptyset$(空集合)は使えるようになったので、$\emptyset$(空集合)という要素に対して「対の公理」が主張する集合を確認できます。上記の$x=\emptyset$の場合ということです。
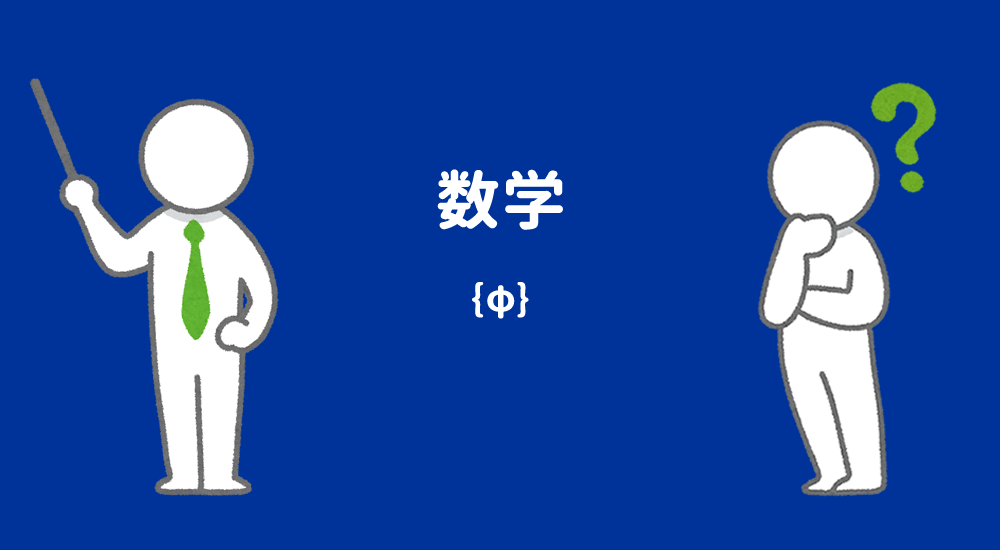
よって、$\{\emptyset\}$という集合(空集合だけを要素に持つ集合)の存在を確認することができました。
ここまでで確認できた集合
- $\emptyset$(空集合)
- $\{\emptyset\}$(空集合だけを要素に持つ集合)
正しく証明・計算の結果が学術的に本当に正しいかどうかは保証できません…ご了承くださいm(__)m
学生の方であれば、疑問に思ったところなどは教授・助教授、その他周りの方に確認してくださいね。
もし、コメント等でご指摘いただければ有難いです。