令和2年センター本試＞数１＞第2問 [1] 再度解いてみた

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

備考

下記のように回答しましたが、実際は二次方程式の種類によってどのようなグラフになるか覚えておくのが一番早いです…。

ただ、忘れてしまったが、時間がある場合は、下記のような流れでも答えにはたどり着くと思います。諦めずに知っていることだけで解くのは大切かなと思います。

最初の回答

第２問 [1]（１）

どのような放物線かを考$\displaystyle -\frac{a^2}{4}+t^2+b$えるために、$y=0$のときを考える。$y=0$とは、$x$軸と交わる点である。

$y=0$のときを考える

$y=x^2+ax+b$が$y=0$のときを考える。

$\displaystyle 0=x^2+ax+b$

$y=0$のとき$x$の値がどうなるか知りたいので、解の公式より、
$\displaystyle x=\frac{-a \pm \sqrt{a^2 -4b } }{2}$

よって、$(\displaystyle \frac{-a + \sqrt{a^2 -4b } }{2}, \, 0)$と$(\displaystyle \frac{-a – \sqrt{a^2 -4b } }{2}, \, 0)$の2点を通ることが分かった。

$x$方向の中点を考える

$\displaystyle \frac{-a + \sqrt{a^2 -4b } }{2}$と$\displaystyle \frac{-a – \sqrt{a^2 -4b } }{2}$の真ん中なので、2つの値を足して半分にすれば良い。

$y=x^2+ax+b$に$\displaystyle x=-\frac{a}{2}$を代入すると、

$\displaystyle y=(-\frac{a}{2})^2-a\frac{a}{2}+b$

$\displaystyle =\frac{a^2}{4}-\frac{a^2}{2}+b$

$\displaystyle =-\frac{a^2}{4}+b$

中点は$\displaystyle (-\frac{a}{2}, \, -\frac{a^2}{4}+b)$

中点から$x$方向（左右）に$t$（$t$は任意の実数）だけずらした点

この点の$y$の値が等しければ、中点を頂点とした左右対称のグラフである。

中点（$x$）$\displaystyle -\frac{a}{2}$を$t$だけずらすので、

$\displaystyle x=-\frac{a}{2}+t$と$\displaystyle x=-\frac{a}{2}-t$を調べる。

$\displaystyle x=-\frac{a}{2}+t$の場合

$y=x^2+ax+b$に$\displaystyle x=-\frac{a}{2}+t$を代入すると、

$\displaystyle y=(-\frac{a}{2}+t)^2+a(-\frac{a}{2}+t)+b$

$\displaystyle =(\frac{a^2}{4}-at+t^2)-\frac{a^2}{2}+at+b$

$\displaystyle =-\frac{a^2}{4}+t^2+b$

$\displaystyle x=-\frac{a}{2}-t$の場合

$y=x^2+ax+b$に$\displaystyle x=-\frac{a}{2}-t$を代入すると、

$\displaystyle y=(-\frac{a}{2}-t)^2+a(-\frac{a}{2}-t)+b$

$\displaystyle =(\frac{a^2}{4}+at+t^2)-\frac{a^2}{2}-at+b$

$\displaystyle =-\frac{a^2}{4}+t^2+b$

左右対称かつ放物線

$\displaystyle x=-\frac{a}{2}+t$と$\displaystyle x=-\frac{a}{2}-t$のどちらも$y$の値は$\displaystyle -\frac{a^2}{4}+t^2+b$となる。

よって、左右対称のグラフであることが分かった。

また、$\displaystyle y=-\frac{a^2}{4}+t^2+b$は$t^2$だけが変数であり、$\displaystyle -\frac{a^2}{4}+b$は定数である。よって、定数は$y$軸方向にずらすだけでグラフの形には影響を与えない。よって、グラフの形は$t^2$を考えればよく、$t^2$は下に凸の放物線なので、$y=x^2+ax+b$も同様に下に凸の放物線である（選択肢：１）。

$x$軸との共有点

上記より、$y=x^2+ax+b$は頂点（下に凸の放物線なので中点は頂点になる）が$\displaystyle (-\frac{a}{2}, \, -\frac{a^2}{4}+b)$の下に凸の放物線である。

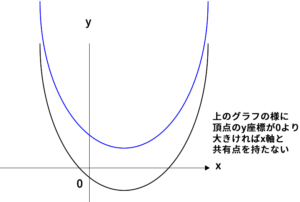
よって、頂点の$y$座標が$0<-\frac{a^2}{4}+b$となるとき、$x$軸との共有点をもたない（。すなわち、$a^2>4b$のとき、$F$と$x$軸は共有点をもたない（選択肢：３）。

スポンサーリンク