
等比数列の和の公式覚えていますか?
$\displaystyle \sum_{k=1}^{n} ar^{k-1}=\frac{a(1-r^n)}{1-r}=\frac{a(r^n-1)}{r-1}$
これが公式です(※真ん中と右辺は変形しただけです、一方だけ覚えておけば十分です)。一定期間であれば覚えておくことができますが、使わないと忘れていきます。
実はこの公式の求め方はとても簡単です。なので、後でも思い出しやすくするために、「どのように導くか」を覚えておきましょう。その方が、テスト中にど忘れしてしまったときでも思い出せる可能性は高くなると思います。
等比数列の和の公式の求め方
初項が$a$、公比が$r$の等比数列$a_n=ar^{n-1}$について考えます。
$n=1$であれば、$a_1=ar^{1-1}=a・1=a$、初項はちゃんと$a$ですね。$n=2$であれば、$a_2=ar^{2-1}=ar$、初項に公比を掛けた値ですね。公比も問題なさそうです。
$\displaystyle \sum_{k=1}^{n} ar^{k-1}$を分解
まず、$a_n=ar^{n-1}$の$1$から$n$までの和$\displaystyle \sum_{k=1}^{n} ar^{k-1}$を分解します。
$\displaystyle =a+ar+ar^2+ \cdots +ar^{n-2}+ar^{n-1}$
両辺に公比の$r$を掛ける
( i ) の両辺に$r$を掛けたものを( ii ) とします。
$r$は公比なので、掛けると各項が自分の次の項の値になります。例えば、初項であれば2項の値に、$n$項であれば$n+1$の項という感じです。
このメリットが何かというと( i )と( ii )の大部分が等しくなるという点です(下図各オレンジ部分)。
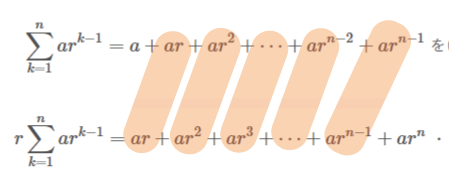
大部分が同じということは各辺の差をとると、大部分が消えてくれるわけです。数学では結構常套手段ですよね。
( i ) ( ii )の各辺を引く
下記( i ) ( ii )の各辺を引きます。
$\displaystyle \sum_{k=1}^{n} ar^{k-1}=a+ar+ar^2+ \cdots +ar^{n-2}+ar^{n-1}$・・・( i )
$\displaystyle r\sum_{k=1}^{n} ar^{k-1}=ar+ar^2+ar^3+ \cdots +ar^{n-1}+ar^n$・・・( ii )
( i ) – ( ii ) の右辺について、先ほど画像でも見たとおり、下記オレンジの部分はすべて等しいので消え、$a$と$ar^n$だけ残ります。
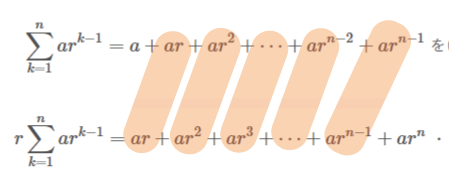
よって、( i ) – ( ii ) は、
$\displaystyle \sum_{k=1}^{n} ar^{k-1} – r\sum_{k=1}^{n} ar^{k-1} =a-ar^{n}$
それぞれ括ると、
$\displaystyle (1-r)\sum_{k=1}^{n} ar^{k-1}=a(1-r^{n})$
従って、下記の通り公式を導き出すことができました。
$\displaystyle \sum_{k=1}^{n} ar^{k-1}=\frac{a(1-r^{n})}{1-r}$
まとめ
解き方は数学でよく出てくるやり方です。等比数列の和の公式の求め方を覚えておいて、いざというときに備えましょう。
単純に公式を覚えるより、少しでも意味がある方が記憶には残りやすいので是非自分で求められるようにしてみてください。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
等比数列、等比数列の和





