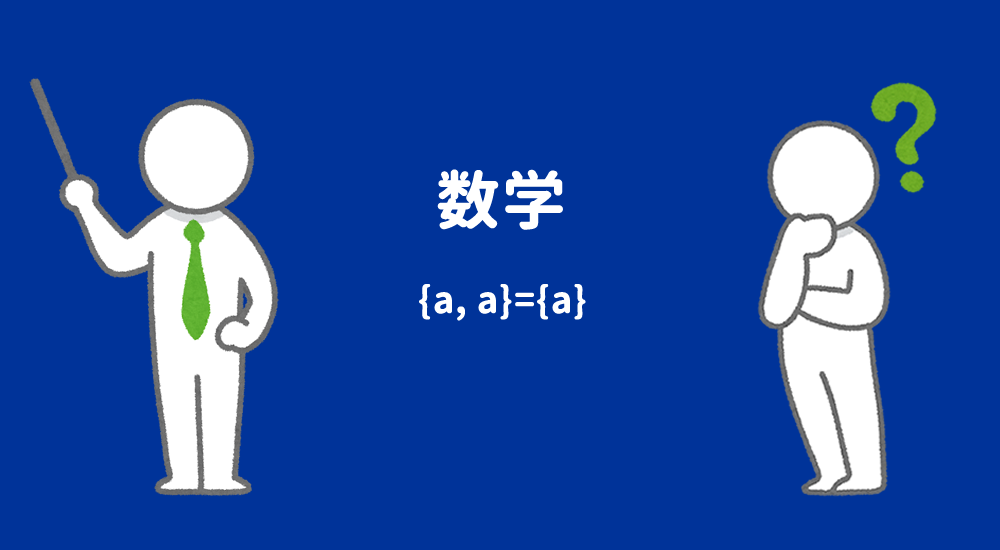
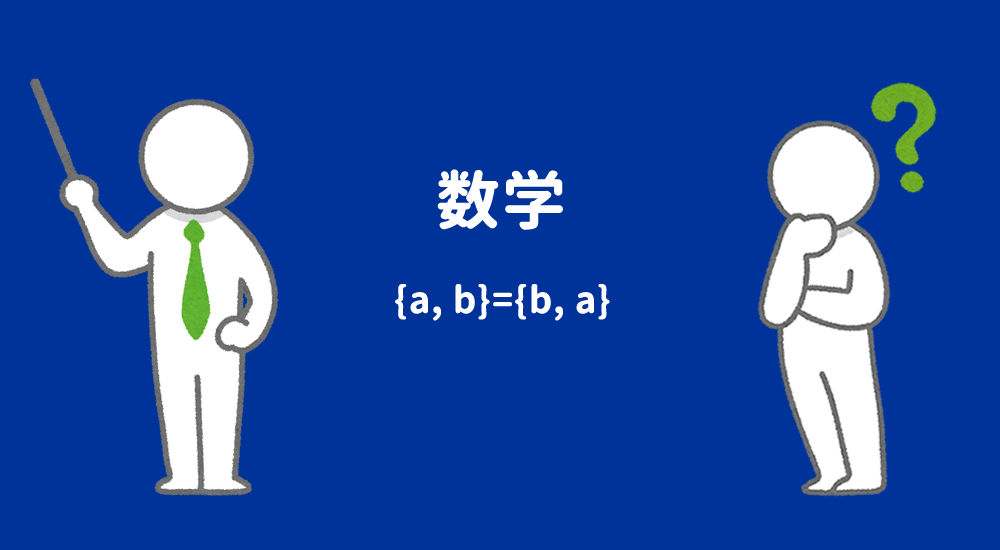
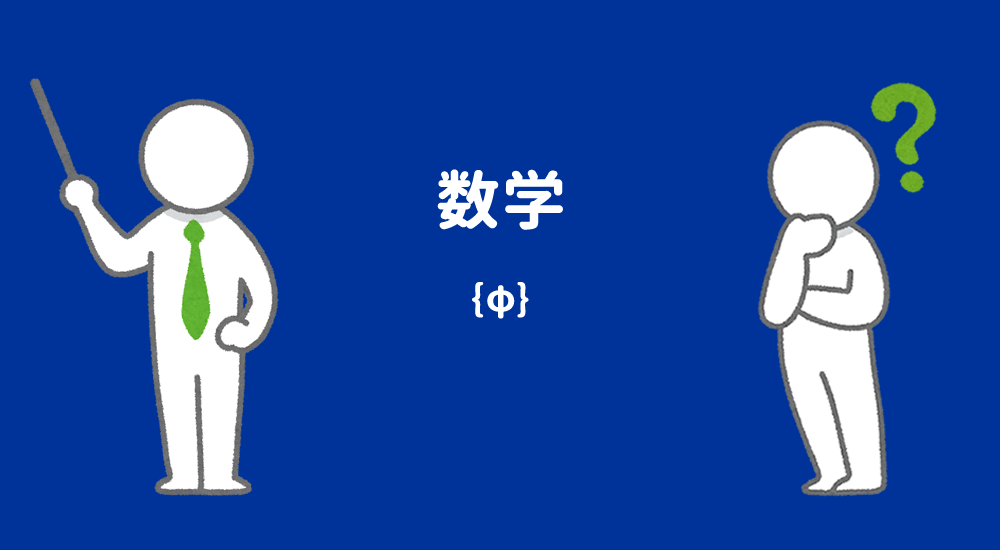
正しく証明・計算の結果が学術的に本当に正しいかどうかは保証できません…ご了承くださいm(__)m
学生の方であれば、疑問に思ったところなどは教授・助教授、その他周りの方に確認してくださいね。
もし、コメント等でご指摘いただければ有難いです。
【問題】外延性の公理の逆含意も成り立つことを証明せよ
外延性の公理の逆含意:$\forall A \, \forall B \, (A = B \to \forall x(x \in A \leftrightarrow x \in B))$が成り立つことを証明せよ
$\forall A \, \forall B \, (\forall x(x \in A \leftrightarrow x \in B) \to A = B)$(任意の集合A、Bが全く同じ要素を持つならば、AとBは等しい)
回答
等式の代入原理によって$\forall A \, \forall B \, (A = B \to \forall x(x \in A \leftrightarrow x \in B))$が成り立つことを証明します。
代入原理: 対象 a, b が a = b であるときには、一つの自由変数 x を含むどんな命題関数 P(x) についても P(a) ⇔ P(b) が(両辺ともに一意的な意味を持つ限りにおいて)常に成り立つ。
ウィキペディアの執筆者,2021,「等式」『ウィキペディア日本語版』,(2021年5月21日取得,https://ja.wikipedia.org/w/index.php?title=%E7%AD%89%E5%BC%8F&oldid=82306340).
$A=B$なので、等式の代入原理より、一つの自由変数$ y$ を含むどんな命題関数$ P(y)$ についても $P(A) \leftrightarrow P(B)$ が成り立ちます。
※外延性の公理にて変数xが使用されているため、自由変数はyに置き換えました
論理式で表すと、$A=B \to (P(A) \leftrightarrow P(B))$・・・(1)が成立するということです。
命題変数$P(y)=\forall x(x \in y)$とする
等式の代入原理より、どんな命題関数$P(y)$でも(1)は成り立つので、$P(y)=\forall x(x \in y)$でも成り立ちます。(1)の$P(A)$、$P(B)$を置き換えると、$A=B \to \forall x(x \in A \leftrightarrow x \in B))$となります。
よって、$A=B \to \forall x(x \in A \leftrightarrow x \in B)$が成り立つことを示せました。
従って、外延性の公理の逆含意:$\forall A \, \forall B \, (A = B \to \forall x(x \in A \leftrightarrow x \in B))$が成り立つことが証明できました。
Q.E.D.
スポンサーリンク
備考
等式の代入原理を用いて、外延性の公理の逆含意も成り立つことが分かりました。つまり、$\forall A \, \forall B \, (\forall x(x \in A \leftrightarrow x \in B) \leftrightarrow A = B)$が成り立つ(真となる)ことが分かりました。
空集合の一意性の証明に役立ちそうな気がします。
キーワード
気になる人は調べてみてね。
公理的集合論、外延性の公理、集合、論理式、全称記号($\forall$)、 等号(=)、代入原理、含意($\to$)、逆含意($\gets$)、同値($\leftrightarrow$)、命題変数、命題関数、Q.E.D.
正しく証明・計算の結果が学術的に本当に正しいかどうかは保証できません…ご了承くださいm(__)m
学生の方であれば、疑問に思ったところなどは教授・助教授、その他周りの方に確認してくださいね。
もし、コメント等でご指摘いただければ有難いです。