
チェバの定理とは、三角形と点との関係性の定理です。
下記のように$\bigtriangleup ABC$と点$D$があります。$AD$を通る直線と$BC$との交点を$E$、$BD$を通る直線と$AC$との交点を$F$、$CD$を通る直線と$AB$との交点を$G$とします。
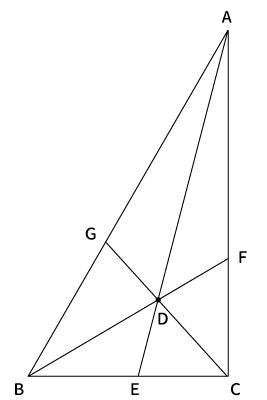
このとき、$\displaystyle \frac{AG}{BG} \frac{BE}{CE} \frac{CF}{AF} = 1$となります。これがチェバの定理です。
今回はメネラウスの定理を使ってチェバの定理を証明したいと思います。通常の証明は「チェバの定理とは?図を用いて分かりやすく証明」をご覧ください。
チェバの定理よりメネラウスの定理の方が証明が簡単な気がします。ですので、まずメネラウスの定理を証明してからチェバの定理を証明する、というのも有りなのかなと思います。不明点があれば、お気軽にコメントください。
では、なんとなく流れが分かっている方が分かりやすいかと思いますので、まずはざっくりとした流れから。
証明のざっくりとした流れ
$\bigtriangleup ABC$の中にできた2つの三角形に対して、メネラウスの定理より2式できて、それを掛け合わせればOK!
もう少し概要をいうと、$\bigtriangleup AEC$と線分$BF$に対してメネラウスの定理を使うと、$\displaystyle \frac{AD}{DE}・\frac{BE}{BC}・\frac{CF}{AF}=1$、

$\bigtriangleup ABE$と線分$CG$に対してメネラウスの定理を使うと、$\displaystyle \frac{AG}{BG}・\frac{BC}{CE}・\frac{DE}{AD}=1$、

メネラウスの定理よりできた2式を各辺掛けると、なんとチェバの定理の形になります。
それでは、詳しく見ていきます。
チェバの定理を「メラネウスの定理」を使って証明
$\bigtriangleup AEC$と線分$BF$に対してメネラウスの定理
線分$AE$によって作れる$\bigtriangleup AEC$と線分$BF$に対して、メネラウスの定理より$\displaystyle \frac{AD}{DE}・\frac{BE}{BC}・\frac{CF}{AF}=1$が成り立ちます。
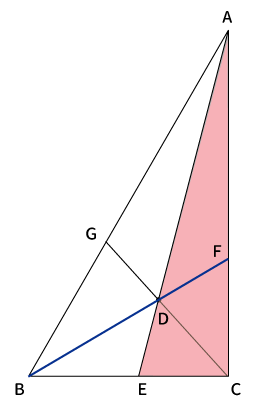
メネラウスの定理は下記のように頂点をスタートにオレンジの矢印の順番に分母・分子×・・・としていくと、それが$1$になるというものです。頂点$A$からスタートした場合だと、$\displaystyle \frac{AD}{DE}・\frac{BE}{BC}・\frac{CF}{AF}=1$ですね。
※スタートは頂点であればどれでもOKです。結果同じ式になります

$\bigtriangleup ABE$と線分$CG$に対してメネラウスの定理
線分$AE$によって作れる$\bigtriangleup ABE$と線分$CG$に対して、メネラウスの定理より$\displaystyle \frac{AG}{BG}・\frac{BC}{CE}・\frac{DE}{AD}=1$が成り立ちます。
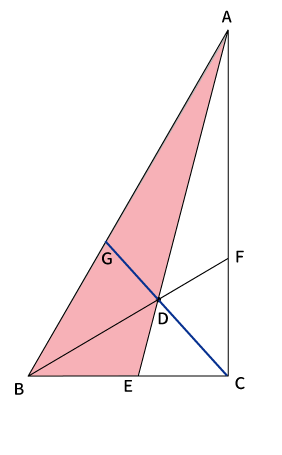
$\bigtriangleup ABE$とと線分$CG$の場合は、下記のような順番です。

メネラウスの定理より求まった2式の各辺を掛ける
メネラウスの定理より
$\bigtriangleup AEC$と線分$BF$に対して、$\displaystyle \frac{AD}{DE}・\frac{BE}{BC}・\frac{CF}{AF}=1$・・・( i )
$\bigtriangleup ABE$と線分$CG$に対して、$\displaystyle \frac{AG}{BG}・\frac{BC}{CE}・\frac{DE}{AD}=1$・・・( ii )
が成り立つことが分かりました。
( i ) ( ii ) の各辺同士を掛けます。
$\displaystyle \frac{BE}{1}・\frac{CF}{AF}・\frac{AG}{BG}・\frac{1}{CE}=1$
$\displaystyle \frac{BE}{CE}・\frac{CF}{AF}・\frac{AG}{BG}=1$
$\displaystyle \frac{AG}{BG}・\frac{BE}{CE}・\frac{CF}{AF}=1$
$\displaystyle \frac{AG}{BG}・\frac{BE}{CE}・\frac{CF}{AF}=1$。チェバの定理が証明できました。
以上で証明終了です。
まとめ
「チェバの定理とは?図を用いて分かりやすく証明」と比べてだだいぶスッキリとした証明になりました。
「メラネウスの定理?図を用いて分かりやすく証明」を先に証明してから、チェバの定理を証明する方法もアリかなと思います。覚えやすい方で2つとも覚えてしまいましょう。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
チェバの定理、メネラウスの定理



