令和2年センター本試＞数１＞第3問 (1) 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第３問（１）

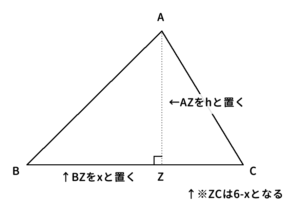
$\bigtriangleup ABC$の$cos \angle ABC$、$sin \angle ABC$を求めるためには、下記$AZ$の値が必要である。
※$Z$は$A$から線分$BC$に対して垂線を下ろし、交わった点

三平方の定理より

$AB=5$、$BC=6$、$CA=\sqrt{21}$、$AZ=h$、$BZ=x$、$ZC=6-x$なので、三平方の定理より、

$\bigtriangleup ABZ$に対して、$AZ^2+BZ^2=AB^2$なので

$h^2+x^2=5^2$・・・( i )

$\bigtriangleup AZC$に対して、$AZ^2+ZC^2=CA^2$なので

$h^2+(6-x)^2=\sqrt{21}^2$・・・( ii )

$x$を求める

( i )－( ii )より、$h^2$が消えるので、$x$が求められる

$h^2+x^2-(h^2+(6-x)^2)=5^2-\sqrt{21}^2$

$\displaystyle x=\frac{10}{3}$

$h$を求める

( i )に$\displaystyle x=\frac{10}{3}$を代入して、$h$を求める

$\displaystyle h^2+(\frac{10}{3})^2=5^2$

$\displaystyle h=\pm \frac{5\sqrt{5}}{3}$

ただし、$h$は三角形の辺なので正の数である。

よって、$\displaystyle h=\frac{5\sqrt{5}}{3}$

$cos \angle ABC$、$sin \angle ABC$を求める

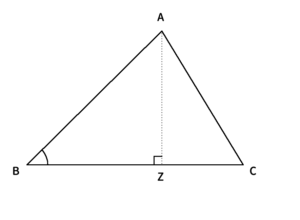
$\displaystyle cos \angle ABC=\frac{AB}{BZ}=\frac{\frac{10}{3}}{5}=$$\displaystyle \frac{2}{3}$

$\displaystyle sin \angle ABC=\frac{AB}{AZ}=\frac{\frac{5\sqrt{5}}{3}}{5}=$$\displaystyle \frac{\sqrt{5}}{3}$

$\bigtriangleup ABC$の面積を求める

$\bigtriangleup ABC$の面積$=BC \times AZ \div 2$で求まる

$\displaystyle 6 \times \frac{5\sqrt{5}}{3} \div 2=$$5\sqrt{5}$

スポンサーリンク