令和2年センター本試＞数１A＞第3問 [1] 解いてみた

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第3問 [1]

選択肢０

1枚のコインを投げる試行を5回繰り返すので、全部で$2^5=32$通りのパターンがある。

「少なくとも1回は表が出る」とは「1度も表が出ない」パターン以外のことである。「1度も表が出ない」パターンは5回とも裏の1パターンのみである。従って、「少なくとも1回は表が出る」パターンは$32-1$の$31$パターンである。

よって、少なくとも1回は表が出る確率$\displaystyle p=\frac{31}{32}=0.96875>0.95$

$p>0.95$（選択肢：０）は正しい。

選択肢１

1回の試行で赤球が出る確率を求めるには袋の中の赤球の数を知る必要がある。

選択肢１の文中には「袋の中に赤球と白球が合わせて8個入っている」と書かれているが、各球の数は明記されていないので赤球の数は分からない。

また、球を1個取り出し、色を調べてから戻す試行を5回試したところで、赤球が1つでも、3つでも5回中3回赤球が出る可能性はある。つまり、この試行を何度繰り返そうが赤球の数は分からない。

よって、赤球の数が分からない以上、1回の試行で赤球が出る確率は分からないので「１回の試行で赤球が出る確率は$\displaystyle \frac{3}{5}$」は正しくはない。

選択肢２

箱の中にある5枚のカードから2枚のカードを引く。つまり「5つある中から2つ選ぶ」ので全部で$\displaystyle _5C_2=\frac{5・4}{2}=10$通りのパターンがある。

引いた2枚のカードの「書かれた文字が異なる」とは「書かれた文字が同じ」パターン以外のことである。「書かれた文字が同じ」パターンは「ろ」「ろ」と「は」「は」の2パターンしかないので、「書かれた文字が異なる」パターンは$10-8$の$8$パターンである。

よって、書かれた文字が異なる確率は$\displaystyle \frac{8}{10}=\frac{4}{5}$である（選択肢：２は正しい）。

選択肢３

まず、選択肢の内容を理解する。

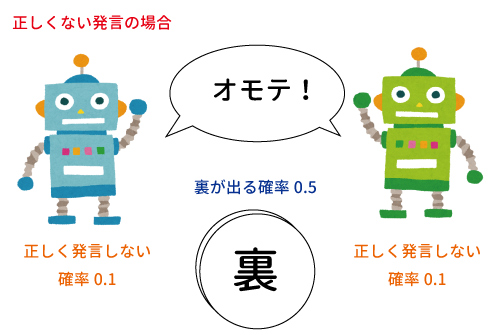
ロボットがコインの出た目を見て、ともに「オモテ」と発言したとき、コインは本当に「表」だった場合と実は「裏」だった場合がある。

コインが「表」だった場合は、ロボットは正しい発言をした時であり、コインが「裏」だった場合は、正しくない発言をした時である。

ロボットがコインの出た目を見て、ともに「オモテ」と発言したときを全体として、そのうち本当にコインが「オモテ」だった場合の確率が$p$が$p \leq 0.9$かどうか問われている。

※下記のようなイメージ

「オモテ」という発言が正しい確率

「オモテ」という発言が正しい確率とは、コインが「表」かつ1体目のロボットが「オモテ」と正しい発言をするかつ2体目のロボットも「オモテ」と正しい発言をする確率である。それぞれの確率は下記の通りである。

これらが同時に起きる確率はこれらを掛ければ良いので、

よって、コインが「表」かつ2体とも「オモテ」と正しい発言をする確率は$\displaystyle \frac{81}{200}$

「オモテ」という発言が正しくない確率

「オモテ」という発言が正しくない確率とは、コインが「裏」かつ1体目のロボットが「オモテ」と正しい発言をするかつ2体目のロボットも「オモテ」と正しい発言をする確率である。それぞれの確率は下記の通りである。

これらが同時に起きる確率はこれらを掛ければ良いので、

よって、コインが「裏」かつ2体とも「オモテ」と正しい発言をする確率は$\displaystyle \frac{1}{200}$

2体とも「オモテ」と発言する全体

コインが「オモテ」「ウラ」の2パターンの場合があるので、上記2つの確率を足せば全体となる。

よって、$\displaystyle \frac{81}{200} + \frac{1}{200} = \frac{82}{200}$

確率$p$

出た面を見た2体が、ともに「オモテ」と発言したとき、実際に「オモテ」が出ている確率$p$は下記を求めればよい。

$\displaystyle p = \frac{「オモテ」という発言が正しい確率}{2体とも「オモテ」と発言する確率}$

従って、$p=0.987…>0.9$なので、$p \leq 0.9$（選択肢：３）は正しくない。

以上より、正しい記述は選択肢０と選択肢２である。

スポンサーリンク