#3 対の公理が主張する集合（「空集合」と「空集合だけを持つ集合」を要素に持つ集合など）

「〇〇集合」だけを要素に持つ集合

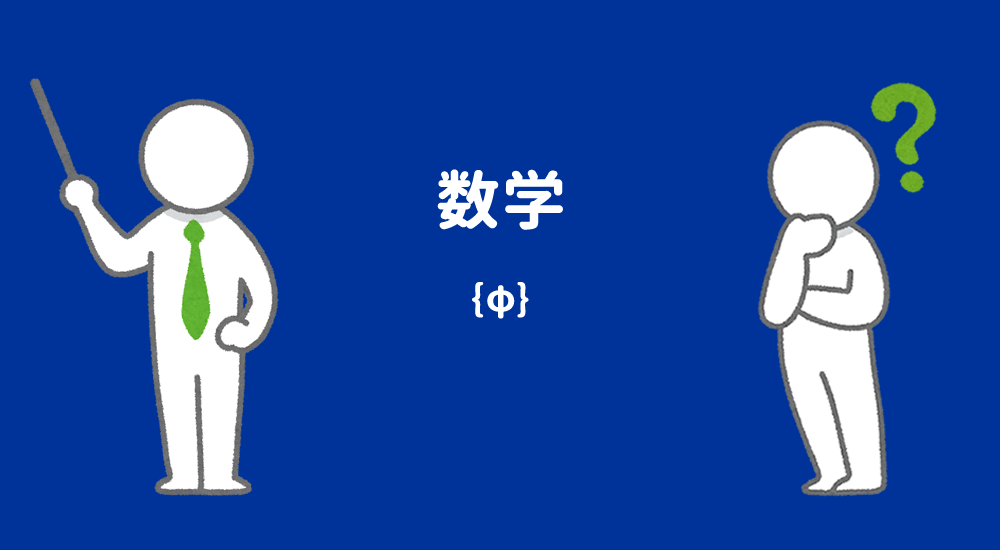
前回、$\{\emptyset\}$（空集合だけを要素に持つ集合）という一元集合を確認しました。

ここで$\{\emptyset\}$に対しても同様に考えると、$\{\{\emptyset\}\}$（「空集合だけを要素に持つ集合」だけを持つ集合）の存在を確認できます。

ということは、$\{\{\{\emptyset\}\}\}$、$\{\{\{\{\emptyset\}\}\}\}$、・・・という集合の存在も確認できます。

「空集合」と「空集合だけを持つ集合」を要素に持つ集合

前々回、前回にて、$\emptyset$（空集合）という集合と$\{\emptyset\}$（空集合だけを要素に持つ集合）の存在が確認できました。

前回見たとおり、「$x$と$y$という要素に対して、対の公理が主張する集合」は1つしか存在しませんので、$\emptyset$と$\{\emptyset\}$に対して、対の公理が主張する集合が存在し、1つに定まり、その集合を$\{ \emptyset, \, \{\emptyset\}\}$と書きます。

対の公理が主張する集合はどんどん増える

これまでに確認した集合は下記のとおりです。

1. $\emptyset$
2. $\{\emptyset\}$
3. $\{\{\emptyset\}\}$、$\{\{\{\emptyset\}\}\}$、$\{\{\{\{\emptyset\}\}\}\}$、・・・
4. $\{\emptyset, \, \{\emptyset\}\}$

このページでは、1から2の集合を作るのと同じ考えで3のような複数の集合を確認できました。また、1、2の集合から4の集合を作りました。

次に、1、2の集合から4の集合を作ったように、上記1～4から2つ要素を選んだ集合の存在も確認できます。

例えば、1と4から、$\{\emptyset, \ \{\emptyset, \, \{\emptyset\}\} \}$、2と3の1つ目から$\{\{\emptyset\}, \ \{\{\emptyset\}\} \}$というように新しい集合を確認できます。

さらに、新しく確認した集合を要素に持つ集合も考えられるので、対の公理が主張する集合はどんどん増えていきます（無限に増える）。

順番が反対の集合は同じ

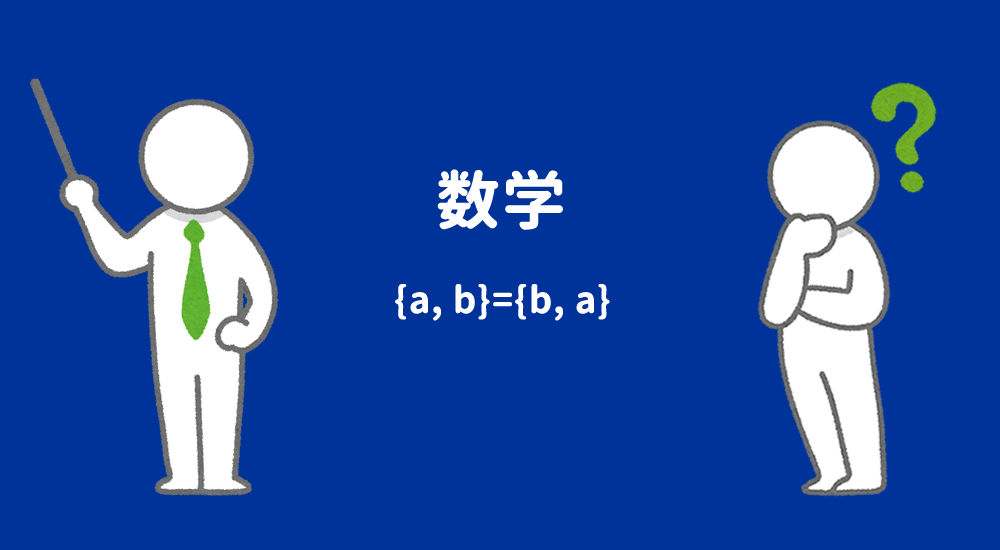
集合{a, b}={b, a}を証明せよより、順番が違う2つの集合が等しいことを確認しています。

ここまでで確認できた集合

1. $\emptyset$（空集合）
2. $\{\emptyset\}$、$\{\{\emptyset\}\}$、$\{\{\{\emptyset\}\}\}$、・・・
   ※一つ左の集合だけを要素に持つ集合
3. $\{\emptyset, \, \{\emptyset\}\}$、$\{\emptyset, \, \{\{\emptyset\}\}\}$、$\{\emptyset, \, \{\{\{\emptyset\}\}\}\}$、・・・
   ※空集合と2の各集合だけを要素に持つ集合
4. $\{\{\emptyset, \, \{\emptyset\}\}\}$、$\{\{\emptyset, \, \{\{\emptyset\}\}\}\}$、$\{\{\emptyset, \, \{\{\{\emptyset\}\}\}\}\}$、・・・
   ※3の各集合だけを要素に持つ集合
5. ・・・

5以降を書くとすると、5「空集合と3の各集合だけを要素に持つ集合」、6「空集合と4の各集合だけを要素に持つ集合」、7「5の各集合だけを要素に持つ集合」、8「6の各集合だけを要素に持つ集合」・・・となります。

2以降に関しては、次回以降、空集合を元に対の公理が主張する集合（無限にある）とします。