
正弦定理とは
△ABC において、BC = a, CA = b, AB = c, 外接円の半径を R とすると、
$\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R$
ウィキペディアの執筆者,2020,「正弦定理」『ウィキペディア日本語版』,(2021年7月20日取得,https://ja.wikipedia.org/w/index.php?title=%E6%AD%A3%E5%BC%A6%E5%AE%9A%E7%90%86&oldid=78821547).

$\bigtriangleup ABC$において、$BC=a$、$CA=b$、$AB=c$、$\angle CAB = \alpha$、$\angle ABC = \beta$、$\angle BCA = \gamma$とし、また$\bigtriangleup ABC$の外接円の半径$AO=R$(外接円の中心を$O$とする)とすると、
$\displaystyle {\frac {a}{\sin \alpha}}={\frac {b}{\sin \beta}}={\frac {c}{\sin \gamma}}=2R$
となることを証明する。
$\displaystyle {\frac {a}{\sin \alpha}}=2R$
$BC$に対して点$B$を通る垂線を引き、その垂線と外接円が交わる点を$D$とすると、直角三角形$\bigtriangleup DBC$が作れる。
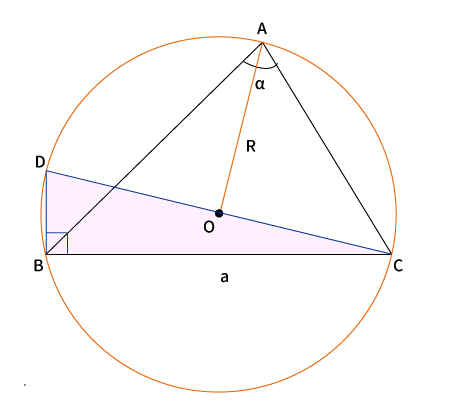
円周角の定理より2つ分かることがある。
( i ) 直角三角形の斜辺は外接円の直径になる
→参考:「円周角が直角のときの性質」
( ii ) 同じ弧に対してどの円周角も等しくなる
→参考:「1つの円弧に対する円周角はどの円周角も等しくなる」
円周角の定理より、$DC$は外接円の直径なので$2R$、$\angle BDC $も$\angle BAC $と同じく弧$\stackrel{\huge\frown}{BC}$に対する円周角なので、$\angle BDC =\angle BAC = \alpha$である。
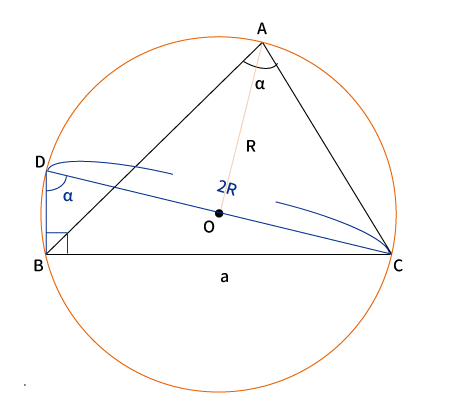
よって、$\displaystyle \sin \alpha = \frac{a}{2R}$
変形すると、$\displaystyle 2R = \frac{a}{\sin \alpha}$
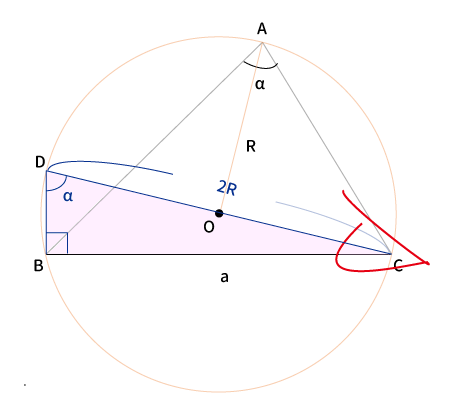
$\displaystyle {\frac {b}{\sin \beta}}=2R$、$\displaystyle {\frac {c}{\sin \gamma}}=2R$
$\displaystyle {\frac {b}{\sin \beta}}=2R$、$\displaystyle {\frac {c}{\sin \gamma}}=2R$も$\displaystyle {\frac {a}{\sin \alpha}}=2R$と全く同じ手順で求められる。
よって、
$\displaystyle {\frac {a}{\sin \alpha}}=2R$、$\displaystyle {\frac {b}{\sin \beta}}=2R$、$\displaystyle {\frac {c}{\sin \gamma}}=2R$
つまり、$\displaystyle {\frac {a}{\sin \alpha}}$、$\displaystyle {\frac {b}{\sin \beta}}$、$\displaystyle {\frac {c}{\sin \gamma}}$の3つともに$2R$なので、
$\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R$
となり、正弦定理を証明できました。
以下、参考までに、$\displaystyle {\frac {b}{\sin \beta}}=2R$、$\displaystyle {\frac {c}{\sin \gamma}}=2R$も簡単に載せておきます。方法は同じなので特に見る必要はありません。
参考:$\displaystyle {\frac {b}{\sin \beta}}=2R$
$CA$に対して点$C$を通る垂線を引き、その垂線と外接円が交わる点を$D$とすると、直角三角形$\bigtriangleup ADC$が作れる。
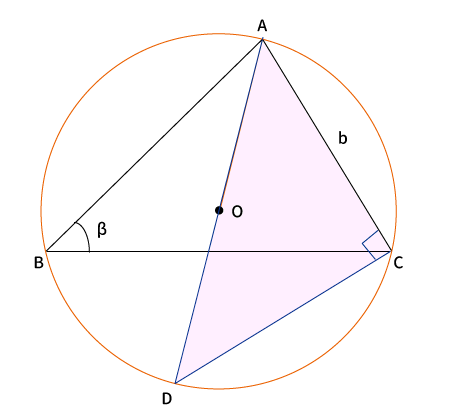
円周角の定理より、$AD$は外接円の直径なので$2R$、$\angle ADC $も$\angle ABC$と同じく弧$\stackrel{\huge\frown}{CA}$に対する円周角なので、$\angle ADC =\angle ABC = \beta$である。
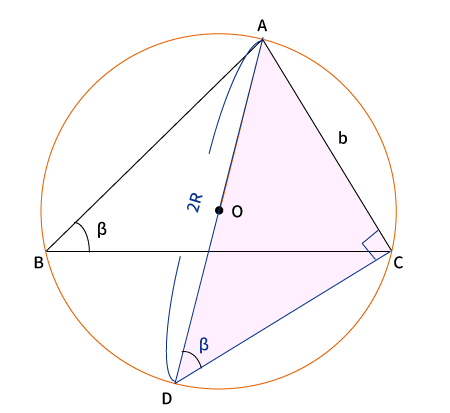
よって、$\displaystyle \sin \beta = \frac{b}{2R}$
変形すると、$\displaystyle 2R = \frac{b}{\sin \beta}$
参考:$\displaystyle {\frac {c}{\sin \gamma}}=2R$
$AB$に対して点$A$を通る垂線を引き、その垂線と外接円が交わる点を$D$とすると、直角三角形$\bigtriangleup ABD$が作れる。

円周角の定理より、$AD$は外接円の直径なので$2R$、$\angle ADB $も$\angle ACB$と同じく弧$\stackrel{\huge\frown}{AB}$に対する円周角なので、$\angle ADB =\angle ACB = \gamma$である。
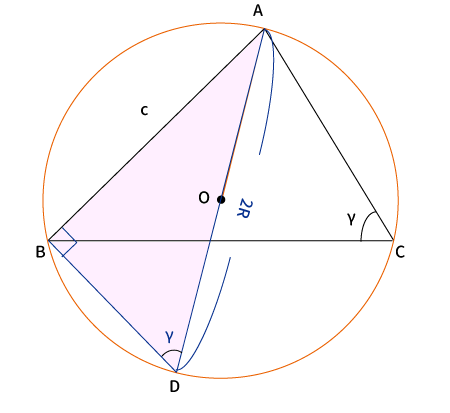
よって、$\displaystyle \sin \gamma= \frac{c}{2R}$
変形すると、$\displaystyle 2R = \frac{c}{\sin \gamma}$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
キーワード
気になる人は調べてみてね。
正弦定理、外接円、円周角の定理




