令和2年センター本試＞数１＞第3問 (2) ( iii ) 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第３問（２）

( iii )$△DHI$の外接円と内接円の半径を求める

$△DHI$の外接円の半径

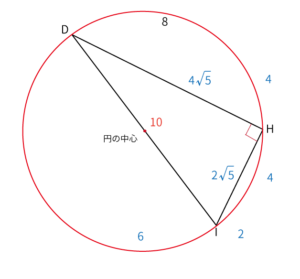
円周角の定理（中心角は円周角の2倍になる）より、直角三角形の斜辺は外接円の直径である。直角三角形の斜辺$DI=10$なので、外接円の直径は$10$。よって、外接円の半径は$5$。

$△DHI$の内接円の半径

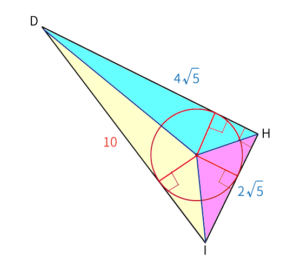
※内接円の中心を$O$、内接円の半径を$r$と置く

内接円の中心$O$から各三角形に垂線を引くと$△ODI$、$△OIH$、$△OHD$の3つの三角形が作れる。この3つの三角形の面積の合計は$△DHI$の面積と等しい。

$△ODI$、$△OIH$、$△OHD$の面積

$△ODI$、$△OIH$、$△OHD$の3つの三角形は円の中心から垂線をおろしてできた三角形なので、高さはすべて内接円の半径$r$である。

よって、$△ODI$、$△OIH$、$△OHD$の各面積を$S1$、$S2$、$S3$と置くと、

$△ODI$の面積${\displaystyle S1=\frac{10r}{2}=5r}$

$△OIH$の面積${\displaystyle S2=\frac{2\sqrt{5}r}{2}=\sqrt{5}r}$

$△OHD$の面積${\displaystyle S3=\frac{4\sqrt{5}r}{2}=2\sqrt{5}r}$

$△DHI$の面積

$△DHI$は直角三角形なので、$△DHI$の面積を$S$と置くと、
$△DHI$の面積${\displaystyle S=2\sqrt{5}\times 4\sqrt{5}÷2=20}$

$S1+S2+S3=S$

$S1+S2+S3=S$なので、
$5r+2\sqrt{5}r+\sqrt{5}r=20$

$△DHI$の内接円の半径$r=3\sqrt{5}-5$

スポンサーリンク