
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
問題
問題は下記を開いてご確認ください。
第2問 (2)
前回より、分かっていることは、
- 放物線$C$:$y=x^2+2x+1$
- 放物線$D$:$y=x^2-(4a-2)x+4a^2+1$
- 直線$l$:$y=2x+1$
2つの放物線$C$、$D$の交点の$x$座標は?
$C$と$D$の交点を$(p, \, q)$と置くと、
$C$:$q=p^2+2p+1$・・・( i )
$D$:$q=p^2-(4a-2)p+4a^2+1$・・・( ii )
( i )から( ii )の各辺を引くと※ ( i ) $-$ ( ii )、
$0=2p+(4a-2)p+1-4a^2-1$
$0=2p+(4a-2)p+1-4a^2-1$
$0=4ap-4a^2$
$-4ap=-4a^2$
$p=a$
$p=a$
よって、交点を$(p, \, q)$の$p$、つまり$x$座標は$a$。
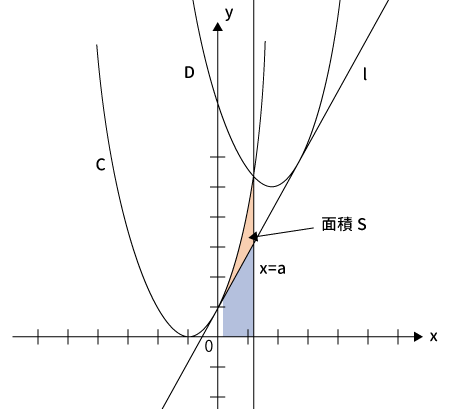
$C$と直線$l$、および$x=a$で囲まれた図形の面積は?
$C$と直線$l$、および$x=a$で囲まれた図形の面積を$S$とする。
(1)の回答より$C$と直線$l$との交点は$(t, \, t^2+2t+1)$に$t=0$を代入すると、$(0, \, 1)$と分かる。
ここでどの部分の面積かをグラフで確認しておく。

※$a>0$より、$D$は$C$より右側にくることが分かる
この面積を求めるには$y=x^2+2x+1$の$0$から$a$の定積分(下図オレンジと青を足した部分)から、下記青色の四角形を引けばよい。青色の方も同様に定積分で計算できる。
定積分
$C$が$y=x^2+2x+1$、直線$l$が$y=2x+1$なので、$C$の方の定積分から直線$l$の定積分を引けばよいので、
$\displaystyle \int_{0}^{a} (x^2+2x+1)dx-\int_{0}^{a} (2x+1)dx$
$\displaystyle \int_{0}^{a} (x^2+2x+1)dx-\int_{0}^{a} (2x+1)dx$
$\displaystyle =\int_{0}^{a} \{x^2+2x+1-(2x+1)\}dx$
※定積分が合体した理由は後述
$\displaystyle =\int_{0}^{a} x^2dx$
$\displaystyle =\left[\frac{x^3}{3}\right]_{0}^{a}$
$\displaystyle =\frac{a^3}{3}$
よって、$S$の面積は、$\displaystyle \frac{a^3}{3}$
$\displaystyle \int_{0}^{a} (x^2+2x+1)dx-\int_{0}^{a} (2x+1)dx$
$\displaystyle =\int_{0}^{a} \{x^2+2x+1-(2x+1)\}dx$
上記のようになることを証明します。つまり、$f(x)=x^2+2x+1$、$g(x)=2x+1$とおいたとき、
$\displaystyle \int_{0}^{a} f(x)dx-\int_{0}^{a} g(x)dx$
また、$f(x)$の導関数を$F(x)$、$g(x)$の導関数を$G(x)$とおきます。すると、
$\displaystyle =\left[F(x)\right]_{0}^{a}-\left[G(x)\right]_{0}^{a}$
$\displaystyle =F(a)-F(0)-(G(a)-G(0))$
$\displaystyle =F(a)-G(a)-F(0)+G(0)$
$\displaystyle =F(a)-G(a)-(F(0)-G(0))$
ここで、$H(X)=F(x)-G(x)$とおくと、
$\displaystyle =H(a)-H(0)$
先ほどと反対の手順に進めると、
$\displaystyle =\left[H(x)\right]_{0}^{a}$
$\displaystyle =\left[F(x)-G(x)\right]_{0}^{a}$
$F(x)$、$G(x)$を微分するとそれぞれ$f(x)$、$g(x)$なので、
$\displaystyle = \int_{0}^{a} (f(x)-g(x))dx$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています