令和2年センター本試＞数１A＞第1問 [1] 解いてみた

 

第1問 [2] ＞

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第１問 [１]（１）

直線$l:y=(a^2 -2a -8)x + a$の傾きが負となるとは、$(a^2 -2a -8)$が負となることなので、$(a^2 -2a -8)< 0$となる。

因数分解すると、
$(a-4)(a +2)< 0$

$(a-4)(a+2)< 0$となるのは、$(a-4)$、$(a+2)$のどちらか一方がマイナス、もう一方がプラスとなる場合だけである。

よって、「$(a-4)<0$ かつ $(a+2)>0$」または「$(a+2)<0$ かつ $(a-4)>0$」である。
「$(a-4)<0$ かつ $(a+2)>0$」を整理すると「$-2<a<4$」・・・（A）
「$(a+2)<0$ かつ $(a-4)>0$」を整理すると「$a<-2 $かつ $4<a$」・・・（B)

（B)は「$a$が-2より小さい、かつ、4より大きい」（矛盾）、このような$a$は存在しないので、答えは、$-2<a<4$となる。

第１問 [１]（２）

直線$l:y=(a^2 -2a -8)x+a$と$x$軸との交点の$x$座標を$b$とするので、式に反映する。

$x$軸との交点ということは、下図のように、$y=0$、$x=b$ということ。

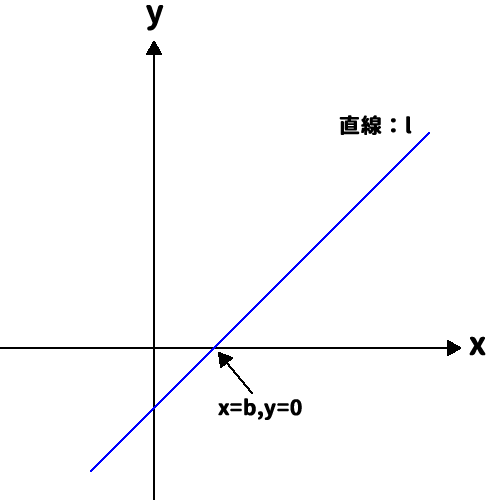
よって、$l:y=(a^2 -2a -8)x+a$に$(b, 0)$を代入すると
$0=(a^2 -2a -8)b+a$となる。

$a>0$の場合

まず、$a>0$の場合に、$b>0$となる$a$の範囲を考える。$b>0$となる場合を考えるので、左辺に$b$をまとめる。

左辺に$b$をまとめると、下記のようになる。

$\displaystyle b=-\frac{a}{(a-4)(a+2)}$

$b>0$より

ここで、$b>0$なので、
$\displaystyle 0< b =-\frac{a}{(a-4)(a+2)}$

よって、下記を満たす$a$の範囲を考えればよい。
$\displaystyle 0<-\frac{a}{(a-4)(a+2)}$

マイナス記号を無くしたいので、少し変形する。両辺に$\displaystyle \frac{a}{(a-4)(a+2)}$を足す。
$\displaystyle \frac{a}{(a-4)(a+2)}<0$

条件より、$a>0$なので、左辺の分子は正となる。よって、分母の$(a-4)(a+2)$が負となればよい。これは先ほど求めた（１）の答えと同じなので、$a$の範囲は$-2<a<4$となる。

ただし、$a>0$という条件もあるため、答えは$0<a<4$となる。

$a \leq 0$の場合

$a >0$と同様に
$\displaystyle \frac{a}{(a-4)(a+2)}<0$

条件より、$a \leq 0$ですが、$a=0$の場合を考える。$a=0$の場合、左辺は$0$となり、$0<0$となるため、$a \neq 0$だと分かる。

次に、$a < 0$を考える。
$a < 0$なので、左辺の分子は負となる。よって、分母の$(a-4)(a+2)$が正となればよい。そして、$(a-4)(a+2)$が正となるのは、$(a-4)$、$(a+2)$がともに正、または、ともに負の場合だけである。

従って、「$(a-4)>0 かつ (a+2)>0$」または「$(a+2)<0 かつ (a-4)<0$」である。
「$(a-4)>0 かつ (a+2)>0$」を整理すると「$4<a$」・・・（A）
「$(a+2)<0 かつ (a-4)<0$」を整理すると「$a<-2$」・・・（B)

条件より、$a \leq 0$なので、（A)は除外され、答えは$a<-2$となる。

$a=\sqrt{3}$のとき

直線$l:y=(a^2 -2a -8)x+a$に$x=b$、$y=0$、$a=\sqrt{3}$を代入すると、

$0=(\sqrt{3}^2 -2\sqrt{3} -8)b+\sqrt{3}$

$\displaystyle b=\frac{5\sqrt{3} \, -6}{13}$

よって、$b$の値は$\displaystyle \frac{5\sqrt{3} \, -6}{13}$となる。

第1問 [2] ＞

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

直線、傾き、因数分解、不等式、交点