
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
問題
問題は下記を開いてご確認ください。
第4問 (3)
- 点$O$を原点とする座標空間に2点$A(3, \, 3, \, -6)$、$B(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$をとる
- 3点$O$、$A$、$B$の定める平面を$\alpha$とする
- $\alpha$に含まれる点$C$は$\overrightarrow{OA} \perp \overrightarrow{OC}$、$\overrightarrow{OB} \cdot \overrightarrow{OC}=24$・・・( i )を満たす
- $|\overrightarrow{OA}|=3\sqrt{6}$
- $|\overrightarrow{OB}|=4\sqrt{3}$
- $|\overrightarrow{OC}| = 2\sqrt{6}$
- $\overrightarrow{OA} \cdot \overrightarrow{OB} = 36$
- $\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$
$\overrightarrow {CB}$は?
$\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$、$B(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$より、$B$から$C$を引けばよいので、
$\overrightarrow {CB}=(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)-(2\sqrt{3}, \, -2\sqrt{3}, \, 0)$
$=(2, \, 2, \, -4)$
ベクトルはどの向きにどのような大きさを持っているかということです。
$\overrightarrow {CB}$の大きさを知る簡単な方法は下図のように、$C$を原点に移動させてしまえば、簡単です。
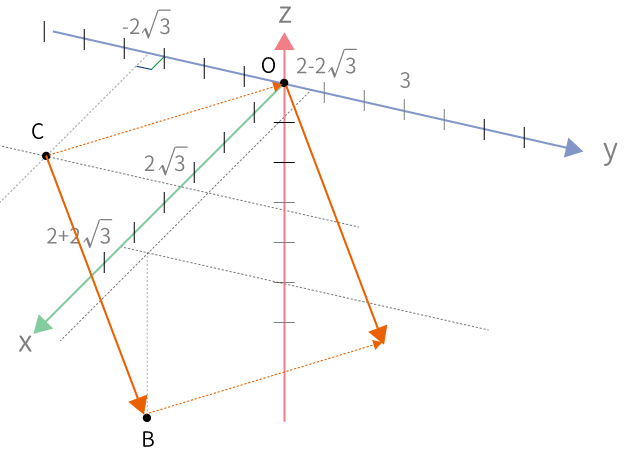
$C$を原点に動かすには$C$の座標をすべて$0$にすれば良いので、$x$、$y$、$z$それぞれ、$(2\sqrt{3}, \, -2\sqrt{3}, \, 0)$分引けば良いのが分かります。
$\overrightarrow {CB}$のスタートが原点にくるように移動するので、もちろん$B$も$(2\sqrt{3}, \, -2\sqrt{3}, \, 0)$分引かなければなりません。
こういった理由で$B$から$C$を引いているわけです。
平面$\alpha$上の四角形$OABC$はどんな四角形?
これまでに分かっていることから絞り込んでいく。
各辺の長さ
まず、下記2つは既に分かっている。
$|\overrightarrow{OA}|=3\sqrt{6}$
$|\overrightarrow{OC}| = 2\sqrt{6}$
$|\overrightarrow {CB}|$を求める
$\overrightarrow {CB}=(2, \, 2, \, -4)$より、
$|\overrightarrow {CB}|^2=2^2+2^2+(-4)^2=24$
よって、$|\overrightarrow {CB}|=\sqrt{24}=2\sqrt{6}$(※絶対値なので正のみ)
$|\overrightarrow {AB}|$を求める
$|\overrightarrow {CB}|$と同じように求めていく。
$A(3, \, 3, \, -6)$、$B(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$より、$B$から$A$を引けばよいので、
$\overrightarrow {AB}=(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)-(3, \, 3, \, -6)$
$=(-1+2\sqrt{3}, \, -1-2\sqrt{3}, \, 2)$
従って、
$|\overrightarrow {AB}|^2=(-1+2\sqrt{3})^2+(-1-2\sqrt{3})^2+2^2$
$=1+12+1+12+4=30$
よって、$|\overrightarrow {AB}|=\sqrt{30}$(※絶対値なので正のみ)
$|\overrightarrow{OA}|=3\sqrt{6}$
$|\overrightarrow{OC}| = 2\sqrt{6}$
$|\overrightarrow {CB}|=2\sqrt{6}$
$|\overrightarrow {AB}|=\sqrt{30}$

各辺の長さが分かり、選択肢$0$~$2$が違うことが分かった。
異なる長さの辺があるので、正方形ではない(選択肢:$0$)。向かい合う辺の長さが等しくないので、長方形でもない(選択肢:$1$)。同様の理由で、平行四辺形でもない(選択肢:$2$)。
あとは、向かい合う辺が平行な個所があるかどうかによって、$3$か$4$かが決まる。
$OA$と$CB$は平行?
$A(3, \, 3, \, -6)$より、$\displaystyle \overrightarrow{OA} = (3, \, 3, \, -6)$、また$\overrightarrow {CB}=(2, \, 2, \, -4)$である。
上記$\displaystyle \overrightarrow{OA}$、$\overrightarrow {CB}$の2つが、実数$u$に対して、$\displaystyle \overrightarrow{OA} = u\overrightarrow {CB}$が成り立てば、$OA$と$CB$は平行だといえる。
$\displaystyle \overrightarrow{OA}$が$\overrightarrow {CB}$の何倍で表せるということは、長さ(大きさ)は異なるが、ベクトルの方向は同じということである。
まず、$x$座標の倍率をチェックすると、$\displaystyle 3 \div 2=\frac{3}{2}$となる。つまり$\overrightarrow{OA}$の$x$座標の値は$\overrightarrow{OB}$の$x$座標の値の$\displaystyle \frac{3}{2}$倍であることが分かった。
$\displaystyle \frac{3}{2} \times \overrightarrow {CB}$を計算してみると、
$\displaystyle \frac{3}{2} \overrightarrow {CB}=\frac{3}{2}(2, \, 2, \, -4)$
$\displaystyle =(3, \, 3, \, -6)$
$\displaystyle (3, \, 3, \, -6)$は$\displaystyle \overrightarrow{OA}$なので、$\displaystyle \overrightarrow{OA} = \frac{3}{2}\overrightarrow{CB}$が成り立った。
従って、$OA$と$CB$は平行である。

問題に「少なくとも一組の対辺が平行な四角形を台形という」とあるので、四角形$OABC$は平行四辺形ではないが、台形(選択肢:3)である。
四角形$OABC$の面積は?
$\overrightarrow{OA} \perp \overrightarrow{OC}$かつ$OA$と$CB$は平行なので、高さは$|\overrightarrow{OC}| = 2\sqrt{6}$である。
そして、上辺と下辺は$|\overrightarrow{OA}|=3\sqrt{6}$、$|\overrightarrow {CB}|=2\sqrt{6}$なので、台形$OABC$の面積は
$(|\overrightarrow{OA}| + |\overrightarrow {CB}|) \times |\overrightarrow{OC}| \div 2$
$=(3\sqrt{6} + 2\sqrt{6}) \times 2\sqrt{6} \div 2$
$=5\sqrt{6} \times \sqrt{6} =30$
四角形$OABC$の面積は$30$。
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています