
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています
問題
問題は下記を開いてご確認ください。
第4問 (4)
- 点$O$を原点とする座標空間に2点$A(3, \, 3, \, -6)$、$B(2+2\sqrt{3}, \, 2-2\sqrt{3}, \, -4)$をとる
- 3点$O$、$A$、$B$の定める平面を$\alpha$とする
- $\alpha$に含まれる点$C$は$\overrightarrow{OA} \perp \overrightarrow{OC}$、$\overrightarrow{OB} \cdot \overrightarrow{OC}=24$・・・( i )を満たす
- $|\overrightarrow{OA}|=3\sqrt{6}$
- $|\overrightarrow{OB}|=4\sqrt{3}$
- $|\overrightarrow{OC}| = 2\sqrt{6}$
- $\overrightarrow{OA} \cdot \overrightarrow{OB} = 36$
- $\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$
点$D$の座標は?
$\overrightarrow {OA} \perp \overrightarrow {OD}$、$\overrightarrow{OC} \cdot \overrightarrow{OD}=2\sqrt{6}$
まず、$\overrightarrow {OD} = (a, \, b, \, 1)$とおく。
$A(3, \, 3, \, -6)$、$\overrightarrow {OA} \perp \overrightarrow {OD}$より、
$\overrightarrow {OA} \cdot \overrightarrow {OD}= 0$なので、
$3a + 3b -6 = 0$
$a = 2 – b$・・・( ii )
$\displaystyle \overrightarrow{OC} = (2\sqrt{3}, \, -2\sqrt{3}, \, 0)$、$\overrightarrow{OC} \cdot \overrightarrow{OD}=2\sqrt{6}$より、
$2\sqrt{3}\, a \, -\, 2\sqrt{3}\, b = 2\sqrt{6}$・・・( iii )
( iii ) に ( ii )を代入すると、
$2\sqrt{3}\, (2 – b) \, -\, 2\sqrt{3}\, b = 2\sqrt{6}$
$2\sqrt{3}\, (2 – b) \, -\, 2\sqrt{3}\, b = 2\sqrt{6}$
$4\sqrt{3}\, -2\sqrt{3}b \, -\, 2\sqrt{3}\, b = 2\sqrt{6}$
$-4\sqrt{3}b = 2\sqrt{6} – 4\sqrt{3}$
$-2b = \sqrt{2} – 2$
$\displaystyle b = 1-\frac{\sqrt{2}}{2}$
$\displaystyle b = 1-\frac{\sqrt{2}}{2}$
これを( ii )$a = 2 – b$に代入すると、
$\displaystyle a = 2 – (1-\frac{\sqrt{2}}{2})$
$\displaystyle a = 1 +\frac{\sqrt{2}}{2}$
よって、$D$の座標は$\displaystyle (1 +\frac{\sqrt{2}}{2}, \, 1-\frac{\sqrt{2}}{2} , \, 1)$
$\angle COD$の値は?
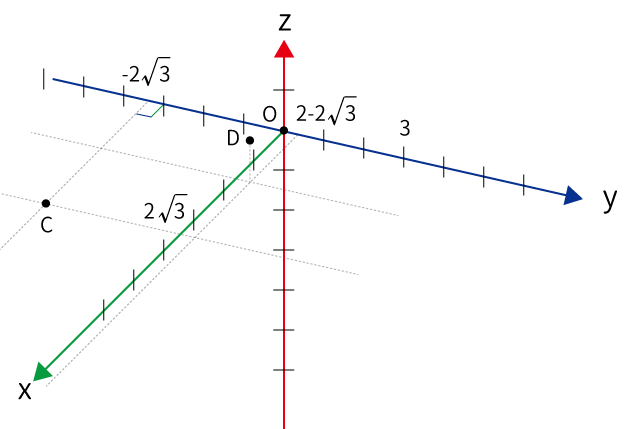
図をかいてみても分からないので、3辺の長さを元に余弦定理から角度を調べる。
関連記事:余弦定理の理解を深める
$OD$の長さは?
次に先ほど求めた$D$の座標は$\displaystyle (1 +\frac{\sqrt{2}}{2}, \, 1-\frac{\sqrt{2}}{2} , \, 1)$より、
$\displaystyle |\overrightarrow{OD}| = (1 +\frac{\sqrt{2}}{2})^2+( 1-\frac{\sqrt{2}}{2})^2+ 1$
$\displaystyle |\overrightarrow{OD}|^2 = (1 +\frac{\sqrt{2}}{2})^2+( 1-\frac{\sqrt{2}}{2})^2+ 1$
$\displaystyle = 1 +\frac{1}{2}+1 +\frac{1}{2}+ 1$
$\displaystyle = 4$
よって、
$\displaystyle |\overrightarrow{OD}| = 2$(※絶対値なので正のみ)
$|\overrightarrow{OD}| = 2$
$\overrightarrow {OC} \cdot \overrightarrow{OD}=|\overrightarrow {OC}| \cdot |\overrightarrow{OD}| \cos \angle COD$なので、
$\overrightarrow{OC} \cdot \overrightarrow{OD}=2\sqrt{6}$、$|\overrightarrow{OC}| = 2\sqrt{6}$、$|\overrightarrow{OD}| = 2$を代入すると、
$2\sqrt{6} = 2\sqrt{6} \cdot 2 cos \angle COD$
$2\sqrt{6} = 2\sqrt{6} \cdot 2 cos \angle COD$
$ 2\sqrt{6} \cdot 2 cos \angle COD = 2\sqrt{6}$
$ 2 cos \angle COD = 1$
$ \displaystyle cos \angle COD = \frac{1}{2}$
$ \displaystyle 0^{\circ} < \angle COD < 180^{\circ}$なので、
$ \displaystyle \angle COD = 60^{\circ}$
$ \displaystyle \angle COD = 60^{\circ}$
三角形$ABC$を底面とする四面体$DABC$の高さは?
3点$O$、$C$、$D$の定める平面を$\beta$とする。$\alpha$と$\beta$は垂直である。
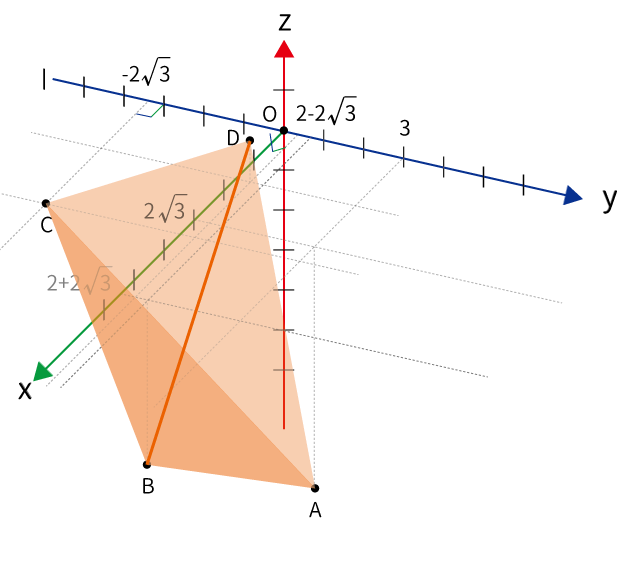
一先ず図示してみたが、整理してみる。
これまでを整理しながら
3点$O$、$A$、$B$を定める平面が$\alpha$である。尚且つ、$C$も$\alpha$に含まれるので、$\bigtriangleup ABC$も$\alpha$に含まれる。
$\overrightarrow{OA} \perp \overrightarrow{OD}$なので、3点$O$、$C$、$D$の定める平面$\beta$は$\alpha$と垂直となる。
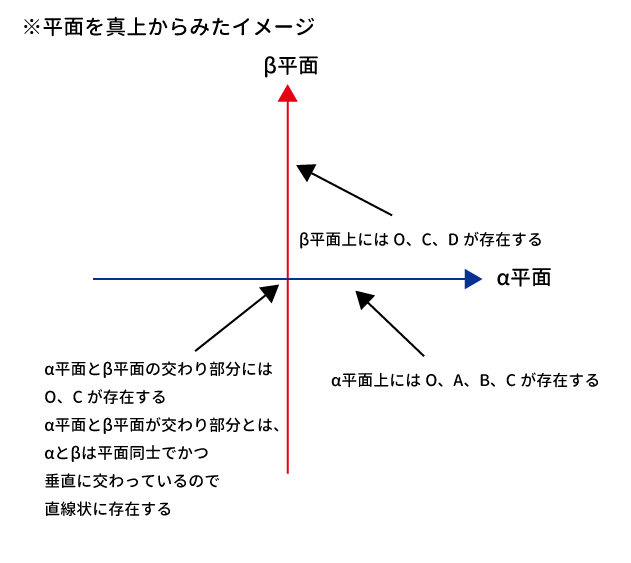
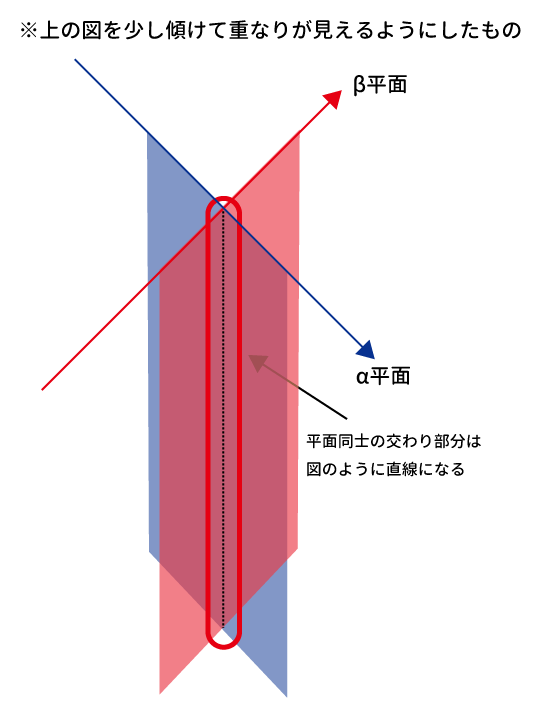
点$D$から平面$\alpha$に垂線を下ろしてできる交点をEとするとき、三角形$ABC$を底面とする四面体$DABC$の高さは$DE$となる。
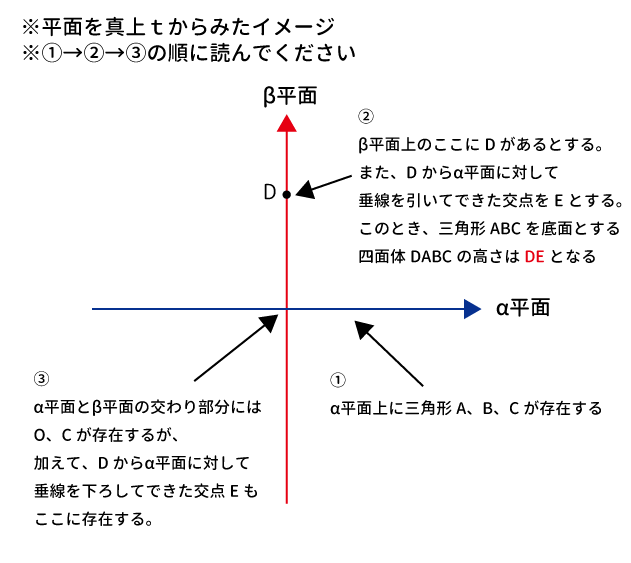
点$O$、$C$、$D$、$E$の関係を図示すると、下記のようになり、$\angle COD=60^{\circ}$なので$1:2:\sqrt{3}$より$DE=\sqrt{3}$(DE:三角形$ABC$を底面とする四面体$DABC$の高さ)

四面体$DABC$の体積は?
上記より、三角形$ABC$を底面とする四面体$DABC$の高さが$\sqrt{3}$と分かっている。つまり、$\bigtriangleup ABC$の面積が分かれば体積は分かる。
$\bigtriangleup ABC$の面積は前回(第4問 (3))で$OABC$が2か所が$90^{\circ}$の台形という点と各辺の長さが分かっていることから求められる。
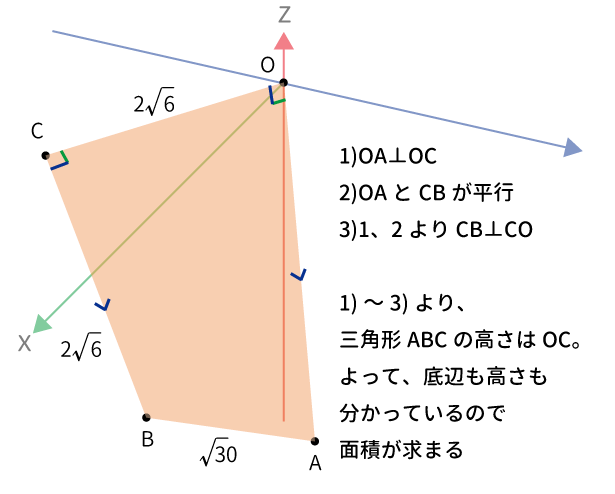
上記より、三角形$ABC$の底辺を$BC$とすると、高さは$OC$なので、
三角形$ABC$の面積$=2\sqrt{6} \cdot 2\sqrt{6} \div 2 = 12$
よって、四面体$DABC$の体積は底面積×高さ÷3なので、
四面体$DABC$の体積は$=12 \times \sqrt{3} \div 3 = 4\sqrt{3}$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています