【問題】二項定理を証明せよ－初等代数学

【問題】二項定理を証明せよ

二項定理$\displaystyle (x+y)^n=\sum_{k=0}^{n}  {}_n C_k \, x^{n-k}y^k$を証明せよ

回答

帰納法によって証明します。

（１）$n=0$のとき

$\displaystyle (x+y)^0=\sum_{k=0}^{0}  {}_0 C_k \, x^{0-k}y^k$

$1={}_0 C_0 \, x^{0}y^0=1×1×1=1$

$n=0$のとき、$\displaystyle (x+y)^n=\sum_{k=0}^{n}  {}_n C_k \, x^{n-k}y^k$は成り立ちました。

（２）$n=1$のとき

$\displaystyle (x+y)^1=\sum_{k=0}^{1}  {}_1 C_k \, x^{1-k}y^k$

$\displaystyle x+y={}_1 C_0 \, x^{1-0}y^0 + {}_1 C_1 \, x^{1-1}y^1$

$=(1×x×1) +(1× 1×y)=x+y$

$n=1$のとき、$\displaystyle (x+y)^n=\sum_{k=0}^{n}  {}_n C_k \, x^{n-k}y^k$は成り立ちました。

（３）$n=m-1$のとき（mは3以上の自然数）

$\displaystyle (x+y)^{m-1}=\sum_{k=0}^{m-1}  {}_{m-1} C_k \, x^{m-1-k}y^k$

両辺に$(x+y)$を掛けます。

（左辺）$\displaystyle ＝(x+y)(x+y)^{m-1}=(x+y)^{m}$・・・（ i ）

（右辺）$\displaystyle ＝(x+y)\sum_{k=0}^{m-1}  {}_{m-1} C_k \, x^{m-1-k}y^k$

$\displaystyle \sum_{k=0}^{m-1}  {}_{m-1} C_k \, x^{m-1-k}y^k$を展開します。

$\sum$を展開

分配

$x$、$y$をともに分配します。

共通部分をまとめる

ここで、下記赤、青部分ともに$m-2$個ずつあって、かつ、係数を除いた部分（$x^{m-1-k}y^k$の部分）が一致しています。
※赤は$x^m$を含めば$m-1$個なので、赤部分は$m-1$より1つ少ない$m-2$個となり、青も$y^m$で考えると同様に$m-2$個となります

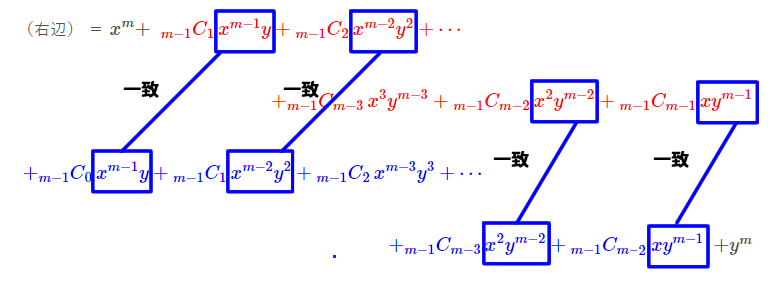
よって、一致している部分をまとめると、

スポンサーリンク

組み合わせを変形

「$\displaystyle {}_n C_r={}_{n-1} C_r+{}_{n-1} C_{r-1}$を証明せよ」より、$\displaystyle {}_n C_r={}_{n-1} C_r+{}_{n-1} C_{r-1}$が成立することが分かっています。従って、上記各赤字を下記のように変形できます。

$\displaystyle {}_{m-1} C_1 + {}_{m-1} C_0 = {}_{m} C_1$

$\displaystyle {}_{m-1} C_2 + {}_{m-1} C_1 = {}_{m} C_2$

$\displaystyle {}_{m-1} C_{m-3} + {}_{m-1} C_{m-4} = {}_{m} C_{m-3}$

$\displaystyle {}_{m-1} C_{m-2} + {}_{m-1} C_{m-3} = {}_{m} C_{m-2}$

$\displaystyle {}_{m-1} C_{m-1} + {}_{m-1} C_{m-2} = {}_{m} C_{m-1}$

上記5つを（ ii ）に代入します。

$\displaystyle + \color{red} {}_{m} C_{m-3} \color{black} \, x^3 y^{m-3} + \color{red} {}_{m} C_{m-2} \color{black} \, x^2 y^{m-2}$

$\displaystyle + \color{red} {}_{m} C_{m-1} \color{black}xy^{m-1} +  y^m$

左辺の形に変形

ここで、$x^m$に$\color{blue} {}_{m} C_0$と$\color{blue} y^0$、$y^m$に$\color{blue} {}_m C_m$、$\color{blue} x^0$を掛けます。

$\displaystyle + {}_{m} C_{m-3} \, x^3 y^{m-3} + {}_{m} C_{m-2} \, x^2 y^{m-2}$

$\displaystyle + {}_{m} C_{m-1}xy^{m-1} + \color{blue} {}_{m} C_m x^0 \color{black} y^m$

$\displaystyle = \sum_{k=0}^{m}  {}_{m} C_k \, x^{m-k}y^k$・・・（ iii ）

まとめ

（ i ）（ iii ）より、$\displaystyle (x+y)^{m-1}=\sum_{k=0}^{m-1}  {}_{m-1} C_k \, x^{m-1-k}y^k$のとき、

$\displaystyle (x+y)^{m} = \sum_{k=0}^{m}  {}_{m} C_k \, x^{m-k}y^k$も成り立ちました。

よって、$n=m-1$のとき、$n=m$も成立することが証明できました。

（１）～（３）より、二項定理$\displaystyle (x+y)^n=\sum_{k=0}^{n}  {}_n C_k \, x^{n-k}y^k$を証明できました。

Q.E.D.

スポンサーリンク

キーワード

気になる人は調べてみてね。

初等代数学、組合せ数学、二項定理、階乗（$!$）、シグマ（$\sum$）、組み合わせ（$\displaystyle {}_{n} C_r$）、Q.E.D.