令和2年センター本試＞数１＞第3問 (3) 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第３問（３）

$\bigtriangleup DHI$を含む平面上にない点$J$は$HJ⊥HD$、$HJ⊥HI$、$HJ=8$なので、$\bigtriangleup HJD$、$\bigtriangleup HJI$は下図のようになる。

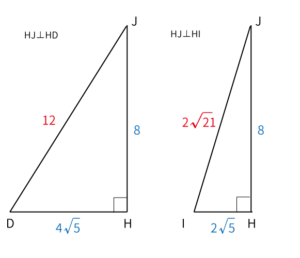
$\bigtriangleup HJD$、$\bigtriangleup HJI$はともに直角三角形なので、三平方の定理より斜辺が求まる。

JDの長さ

$JD^2=HJ^2+DH^2=8^2+4\sqrt{5}^2$

$JD=12$

JIの長さ

$JI^2=HJ^2+IH^2=8^2+2\sqrt{5}^2$

$JI=2\sqrt{21}$

$\bigtriangleup IDJ$の面積

上記より、$\bigtriangleup IDJ$の2辺の長さが$JD=12$、$JI=2\sqrt{21}$だと分かった。また、$ID=10$は既に「数１＞第3問 (2) ( i )  」で分かっている。よって、下記のような図になる。

ここで問題にあるように問３の（１）を考慮するために見返してみる。すると、$\bigtriangleup IDJ$と$\bigtriangleup ABC$の各辺をみてみると、$\bigtriangleup IDJ$は$\bigtriangleup ABC$の各辺の2倍の辺を持っている。

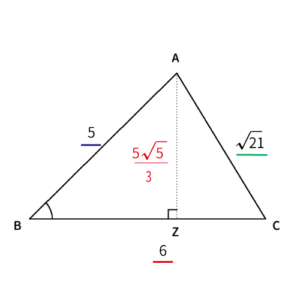
$I$から$DJ$に下ろした垂線の長さ

つまり、$I$から$DJ$に下ろした垂線の長さも$AZ$の2倍の$\displaystyle \frac{10\sqrt{5}}{3}$になる。

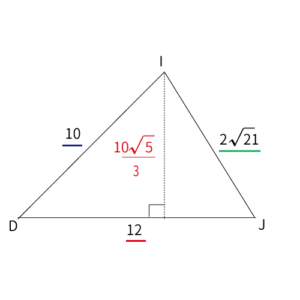
従って、$\bigtriangleup IDJ$の面積は

$\bigtriangleup IDJ$の面積$\displaystyle =12 \times \frac{10\sqrt{5}}{3} \div 2=$$20\sqrt{5}$

点$H$から$\bigtriangleup IDJ$に下ろした垂線$HK$の長さ

一度、四面体$JDHI$がどのような図形かイメージしておく。

 

先ほど面積を求めた面は下図の青い部分になる。この面に対して、$H$から垂線を下ろした$HK$の長さを知りたい。

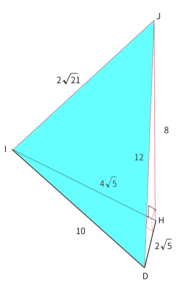
$\bigtriangleup IDJ$と$HK$、$\bigtriangleup DHI$と$JH$からそれぞれ体積を求める

ここで、$\bigtriangleup IDJ$と$HK$、$\bigtriangleup DHI$と$JH$を使って、それぞれ四面体$JDHI$の体積を求める。

体積の値は一致するので、唯一長さが分かっていない$HK$の長さが求まる。
※$\bigtriangleup DHI$は直角三角形で辺の長さが全て明らかなので面積が求まる

$\bigtriangleup IDJ$と$HK$

$\bigtriangleup IDJ$の面積は$20\sqrt{5}$、高さは不明なので$HK$で計算する。

四面体$JDHI$の体積$\displaystyle =20\sqrt{5} \times HK \div 3 = \frac{20\sqrt{5} HK}{3}$・・・( A )

$\bigtriangleup DHI$と$JH$

$\bigtriangleup DHI$の面積は$2\sqrt{5} \times 4\sqrt{5} \div 2 = 20$

高さは$HJ=8$なので、

四面体$JDHI$の体積$\displaystyle =20 \times 8 \div 3 = \frac{160}{3}$・・・( B )

 

( A )( B )より、

$\displaystyle \frac{20\sqrt{5} HK}{3} = \frac{160}{3}$

$\displaystyle HK=\frac{8\sqrt{5}}{5}$

スポンサーリンク