令和2年センター本試＞数１A＞第2問 [2] (1) 解いてみた

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第２問 [２] （１）

四分位相よりまず分かること

四分位相はデータを小さいものから並べて字のとおりデータを均等に4分割したもの。

ここでは99個のデータなので、真ん中の50番目が第2四分位数であり、中央値である。つまり、中央値より小さい観測値の個数は48個である。

次に、第2四分位数より小さい側のデータが49個あるので、その真ん中の25番目が第1四分位数である。第2四分位数より大きい側のデータも同様に49個あるので、その真ん中の25番目、全体だと75番目が第3四分位数である。

四分位相について押えておきたいことはこちら＞

選択肢を一つずつチェックしていく。

選択肢０：平均値は第1四分位数と第3四分位数の間にある

×：平均値は第1四分位数と第3四分位数の間にない場合がある

数が小さい側のデータや大きい側のデータが第1四分位数～第3四分位数の外側に偏っている場合に成立しない。

（反例）1番目から98番目まで、すべて「$0$」、99番目が「$99$」とする。
このとき、平均値は$1$である。98番目が$0$、99番目が$99$なので、平均値は$1$は98番目と99番目の間にある。第1四分位数は25番目、第3四分位数は75番目なので、平均値はその間にはない。

参考：平均値$＝\{(0 \times 98) +99\}\div 99 = 1$

選択肢１：四分位範囲は標準偏差より大きい

×：四分位範囲は標準偏差より小さい場合がある

数が小さい側のデータや大きい側のデータが第1四分位数～第3四分位数の外側に偏っている場合に成立しない。

（反例）1番目のデータから第3四分位数までの数値がすべて「$0$」、第3四分位数の次からすべて$99$とする。
※計算しやすいように99とする

このとき、$\{(0 \times 75) + (99 \times 24)\} \div 99 = 24$なので、平均値は「$24$」

また、四分位範囲は第3四分位数－第1四分位数なので「$0$」

最後に標準偏差はデータのバラツキ具合の平均のようなものなので、各データから平均を引いて2乗した値をすべて足して、それをデータの数で割り、ルートをとったものである。よって、

ここで、標準偏差$\displaystyle \sigma=\sqrt{\frac{76^2 \times 24}{99}}$は分母分子ともに正の数なので$\displaystyle \sqrt{\frac{76^2 \times 24}{99}} > 0$は明らかである。

四分位範囲は「$0$」なので、四分位範囲は標準偏差より小さい。

選択肢２：中央値より小さい観測値の個数は49個である

×：中央値より小さい観測値の個数は49個より小さい場合もある

中央値と同じ値のデータが複数ある場合は、49個より小さくなる。

（反例）1つ目のデータが「$0$」、2つ目以降の値がすべて「$100$」とする。このとき、中央値は「$100$」。「$100$」より小さい値は1つ目のデータしかないので、中央値より小さい観測値の個数は1個である。

選択肢３：最大値に等しい観測値を1個削除しても第１四分位数は変わらない

〇：最大値に等しい観測値を1個削除しても第１四分位数は変わらない

最大値に等しいということは1番後ろのデータを一つ削除すると考えて問題ない。

よって、一番後ろのデータを削除する前と後の第１四分位数を調べる。

データは小さい順から$A1, \, A2, \, A3・・・, \, A97, \, A98, \, A99$とする。最大値と等しい観測値を削除するので、最低でも$A98＝A99$である。

最後のデータを削除しない場合（99個）

第２四分位数が$A50$なので、第２四分位数より小さい側のグループは49個ある。その中の真ん中である$A25$が第１四分位数になる。

最後のデータを削除した場合（98個）

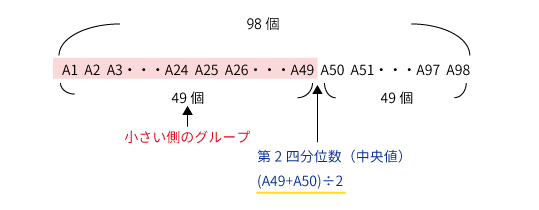
データが偶数個なので、第２四分位数は$(A49+A50)\div 2$である。このとき第２四分位数より小さい側のグループはA49も含むため、49個ある。その中の真ん中である$A25$が第１四分位数になる。

よって、最大値に等しい観測値を1個削除しても第１四分位数は変わらない。

選択肢４：第１四分位数より小さい観測値と、第３四分位数より大きい観測値とをすべて削除すると、残りの観測値は51個である

×：残りの観測値は51個より少なくなる場合がある

第１四分位数や第３四分位数と同じ値のデータが複数ある場合は、51個より小さくなる。

（反例）1番目から98番目まで、すべて「$0$」、99番目が「$99$」とする。
このとき、第１四分位数、第３四分位数はともに$0$である。第１四分位数より小さい観測値はなく、第３四分位数より大きい観測値は99番目（$100$）しかないので、残りの観測値は1個となる。

選択肢５：第１四分位数より小さい観測値と、第３四分位数より大きい観測値とをすべて削除すると、残りの観測値からなるデータの範囲はもとのデータの四分位範囲に等しい

〇：第１四分位数より小さい観測値と、第３四分位数より大きい観測値とをすべて削除すると、残りの観測値からなるデータの範囲はもとのデータの四分位範囲に等しい

四分位範囲

データは小さい順から$A1, \, A2, \, A3・・・, \, A97, \, A98, \, A99$とする。

すると、第３四分位数は$A75$、第１四分位数は$A25$なので、四分位範囲は$A75-A25$となる。

残りの観測値からなるデータの範囲

（ i ）$A24＜A25$かつ$A75＜A76$の場合

この場合、$A24$は$A25$より小さいので$A24$より前はすべて削除、同様に$A76$は$A75$より大きいので$A75$より後ろはすべて削除。

よって、データはA25～A75となる。従って、データの範囲は$A75-A25$となる。これは四分位範囲と等しい。

（ ii ）$A24=A25$かつ$A75=A76$の場合

この場合、$A24$は$A25$と等しいので、$A23$より前をすべて削除、同様に$A76$は$A75$と等しいので$A76$より後ろをすべて削除。

よって、データはA24～A76となる。従って、データの範囲は$A76-A24$となるが、$A24=A25$かつ$A75=A76$の場合なのでデータの範囲は$A75-A25$でもある。これは四分位範囲と等しい。

( iii )$A24=A25$またはh$A75=A76$の場合

（ ii ）$A24=A25$かつ$A75=A76$の場合と同様。データの範囲は$A75-A25$でもあり、四分位範囲と等しい。

回答

以上より、最大値に等しい観測値を1個削除しても第１四分位数は変わらない（選択肢３）、第１四分位数より小さい観測値と、第３四分位数より大きい観測値とをすべて削除すると、残りの観測値からなるデータの範囲はもとのデータの四分位範囲に等しい（選択肢５）の2つが成り立つ。

スポンサーリンク