
問題
問題は下記を開いてご確認ください。
第5問
$\bigtriangleup ABC$において辺$BC$を$7:1$に内分する点を$D$、辺$AC$を$7:1$に内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$FC$と辺$AB$の交点を$G$とすると、次のような図になる。
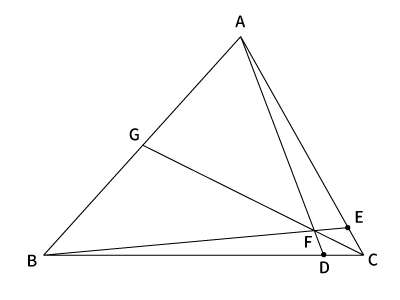
$\bigtriangleup ABC$と点$F$に対して、チェバの定理より$\displaystyle \frac{AG}{GB} ・\frac{BD}{DC}・\frac{CE}{EA}=1$が成り立つ。これを ( i ) とする。
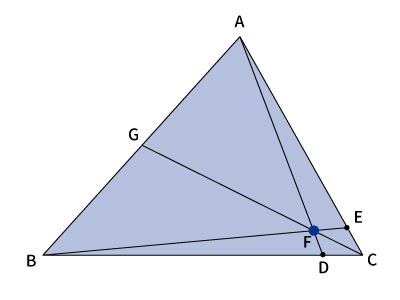
「チェバの定理とは?図を用いて分かりやすく証明」の図を見てみてください。
この問題と点の位置が違うだけでほとんど同じ図形でチェバの定理を使っています。これを知っていれば、すぐにチェバの定理を使うのだということが分かります。
$\displaystyle \frac{GB}{AG}$を求める

辺$BC$を$7:1$に内分する点が$D$なので、$BD$は$DC$の7倍である。よって、$BD=7DC$・・・( ii )
同様に、辺$AC$を$7:1$に内分する点を$E$なので、$EA$は$CE$の7倍である。よって、$EA=7CE$
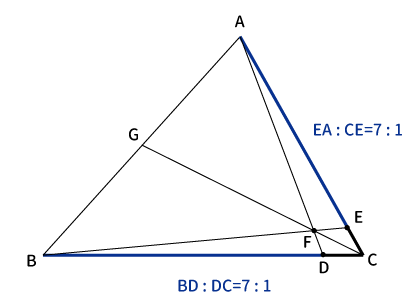
以上より、( i )$\displaystyle \frac{AG}{GB} ・\frac{BD}{DC}・\frac{CE}{EA}=1$ に$BD=7DC$、$EA=7CE$を代入すると、
$\displaystyle \frac{AG}{GB} ・\frac{7DC}{DC}・\frac{CE}{7CE}=1$
$\displaystyle \frac{AG}{GB} ・\frac{7DC}{DC}・\frac{CE}{7CE}=1$
$\displaystyle 1 = \frac{AG}{GB} ・7・\frac{1}{7}$
$\displaystyle \frac{GB}{AG} = 1$
$\displaystyle \frac{GB}{AG} = 1$・・・( iii )
$\displaystyle \frac{FD}{AF}$を求める

$\bigtriangleup ABD$と直線$CG$に対して、メネラウスの定理より、
$\displaystyle \frac{AG}{GB}・\frac{BC}{DC}・\frac{FD}{AF}=1$ が成り立つ。
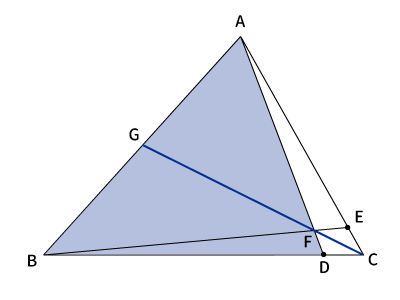
$\displaystyle \frac{AG}{GB}$を求める
( iii )$\displaystyle \frac{GB}{AG} = 1$より、$\displaystyle \frac{AG}{GB} = 1$となる。
$\displaystyle \frac{BC}{DC}$を求める
まず、$BC$は$BD$と$DC$を合わせたものなので、$BC=BD+DC$が成り立つ。

これに( ii ) $BD=7DC$ を代入すると、
$BC=$$BD+DC=7DC+DC=8DC$・・・( iv )
$\displaystyle \frac{BC}{DC}$に↑を代入すると、
$\displaystyle \frac{BC}{DC}=\frac{8DC}{DC}=8$となる。
以上より、$\displaystyle \frac{AG}{GB}・\frac{BC}{DC}・\frac{FD}{AF}=1$に$\displaystyle \frac{AG}{GB} = 1$、$\displaystyle \frac{BC}{DC}=8$を代入すると、
$\displaystyle 1・8・\frac{FD}{AF}=1$
よって、$\displaystyle \frac{FD}{AF}=\frac{1}{8}$・・・( v )
$\displaystyle \frac{FC}{GF}$を求める
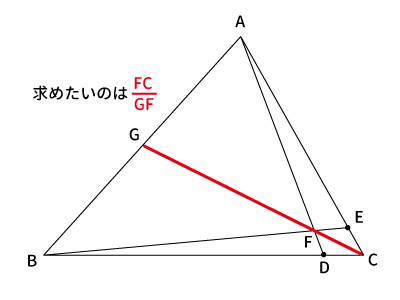
$\bigtriangleup BCG$と直線$AD$に対して、メネラウスの定理より、
$\displaystyle \frac{AG}{AB}・\frac{BD}{DC}・\frac{FC}{GF}=1$ が成り立つ。

$\displaystyle \frac{AG}{AB}$を求める
まず、$AB$は$AG$と$GB$を合わせたものなので、$AB=AG+GB$が成り立つ。

( v )$\displaystyle \frac{GB}{AG} = 1$より、${GB}={AG}$となる。
$AB=AG+GB$に↑を代入すると、$AB=2AG$
よって、$\displaystyle \frac{AG}{AB}$に$AB=2AG$を代入すると、
$\displaystyle \frac{AG}{AB}=\frac{AG}{2AG}=\frac{1}{2}$
$\displaystyle \frac{BD}{DC}$を求める
$\displaystyle \frac{BD}{DC}$に( ii ) $BD=7DC$を代入すると、
$\displaystyle \frac{BD}{DC}=\frac{7DC}{DC}=7$
以上より、$\displaystyle \frac{AG}{AB}・\frac{BD}{DC}・\frac{FC}{GF}=1$に$\displaystyle \frac{AG}{AB}=\frac{1}{2}$、$\displaystyle \frac{BD}{DC}=7$を代入すると、
$\displaystyle \frac{1}{2}・7・\frac{FC}{GF}=1$
よって、$\displaystyle \frac{FC}{GF}=\frac{2}{7}$・・・( vi )
$\displaystyle \frac{\bigtriangleup CDGの面積}{\bigtriangleup BFGの面積}$を求める
求めたいのは下図、青い三角形$\bigtriangleup CDG$、赤い三角形$\bigtriangleup BFG$の面積の比、$\displaystyle \frac{\bigtriangleup CDGの面積}{\bigtriangleup BFGの面積}$である。

三角形の面積を求める必要があるので、それぞれ底辺と高さが必要になる。
既に$\displaystyle \frac{FC}{GF}=\frac{2}{7}$が分かっているので、青い三角形$\bigtriangleup CDG$は$CG$、赤い三角形$\bigtriangleup BFG$は$GF$を底辺とすれば比率が分かる。高さの方も$BD:CD$が分かっているので相似関係から比率が分かる。
底辺
$\displaystyle \frac{FC}{GF}=\frac{2}{7}$より、$\displaystyle FC=\frac{2}{7} GF$である。
また、$CG=FC+GF$なので、$\displaystyle CG=\frac{2}{7} GF+GF=\frac{9}{7} GF$

よって、
$\bigtriangleup BFG$の底辺は$GF$
$\bigtriangleup CDG$の底辺は$\displaystyle \frac{9}{7} GF$
と底辺を$GF$だけを用いて表せた。
高さ
$D$から直線CGに下ろした垂線との交点を$I$としたとき、青い三角形$\bigtriangleup CDG$の高さ$DI$、$B$から直線CGに下ろした垂線との交点を$H$としたとき、赤い三角形$\bigtriangleup BFG$の高さ$BH$である。
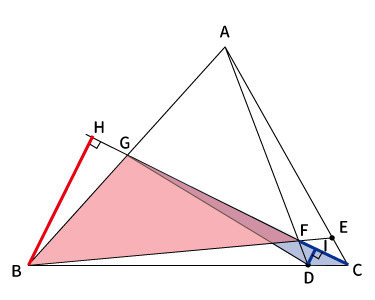
ここで次の緑の三角形$\bigtriangleup BCH$とオレンジの三角形$\bigtriangleup DCI$を見ると、以下より2つの角が同じなので、相似である。
- $\angle BHC$と$\angle DIC$がともに$90^{\circ}$
- $\angle BCH$と$\angle DCI$は同じ角なので等しい
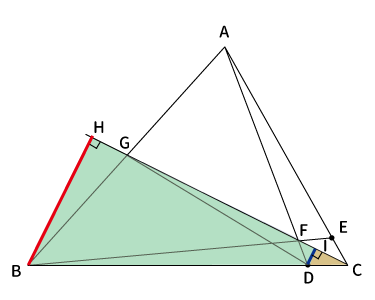
よって、$BH:DI=BC:DC$となるので、$BH・DC=DI・BC$である。
また、( iv )$BC=8DC$を代入すると、$BH・DC=DI・8DC$、
$BH=8DI$となる。
従って、
$\bigtriangleup BFG$の高さは$8DI$
$\bigtriangleup CDG$の高さは$DI$
と高さを$DI$だけを用いて表せた。
$\displaystyle \frac{\bigtriangleup CDGの面積}{\bigtriangleup BFGの面積}$
以上より、各底辺と高さが分かったので、それぞれの面積は、
青い三角形$\bigtriangleup CDG$の面積は、$\displaystyle \frac{9}{7} GF ・ DI$
赤い三角形$\bigtriangleup BFG$の面積は、$\displaystyle GF ・ 8DI=8DI・GF$
よって、$\displaystyle \frac{\bigtriangleup CDGの面積}{\bigtriangleup BFGの面積}$は
$\displaystyle \frac{\frac{9}{7} GF ・ DI}{8DI・GF}=$$\displaystyle \frac{9}{56}$
スポンサーリンク
- 問題の解答例など解法は見ずに解いています。覚えていない部分は学習はしますが、直接問題の解き方は調べていません。
よって、順当な解法かは分かりませんが、何か参考になれば幸いです - なるべく細かく書くようにしています。不明点はコメントいただければ嬉しいです
- また、正解かどうかのチェックは行い、正解にはなっています