令和2年センター本試＞数１A＞第1問 [3] 解いてみた

 

問題

問題は下記を開いてご確認ください。

令和２年度本試験の問題｜大学入試センター

第１問 [３]（１）

グラフ$G$は$y=x^2$を2点$(c, \, 0)$、$(c+4, \, 0)$を通るように平行移動したものである。

グラフ$G$の頂点の$x$座標を求める

図からも分かるように、グラフ$G$の頂点の$x$座標は$c$と$c+4$の真ん中である。

よって、グラフ$G$の頂点$\displaystyle x=\frac{c+4+c}{2}=\frac{2c+4}{2}=c+2$

グラフ$G$の頂点の$y$座標を求める

グラフ$G$の頂点$(c+2, \, ?)$と$(c, \, 0)$の$x$座標方向の差は$(c+2)-c=2$である。

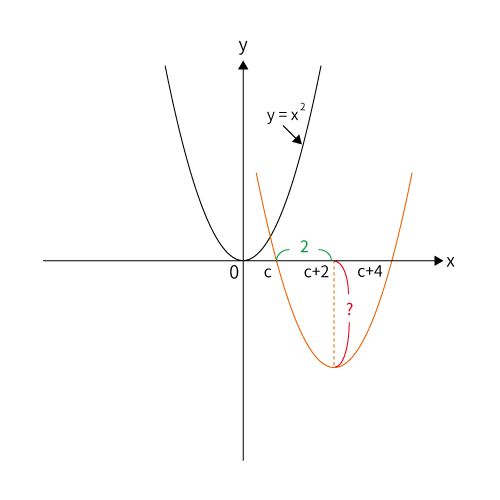
知りたいのは$y$座標の高さ「?」である。これは、グラフ$F$の頂点から$x$軸方向に$2$離れたところの$y$の高さである。プラスでもマイナスでも良いので$x=-2$で計算する。

$y=(-2)^2=4$

よって、高さ「?」は$4$、マイナス方向なので、グラフ$G$の頂点$y=-4$

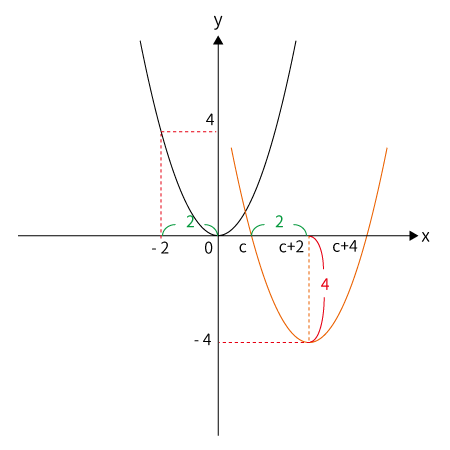
どれくらい平行移動した？

上記より、グラフ$G$の頂点の座標が$(c+2, \, -4)$である。

グラフ$F$の頂点は$(0, \, 0)$なので、グラフ$G$はグラフ$F$を$x$軸方向に$c+2$、$y$軸方向に$-4$平行移動したグラフと分かる。

よって、平行移動の公式より、

$y-(-4)=\{x-(c+2)\}^2$

よって、Gをグラフに持つ2次関数は$y=x^2-2(c+2)x+c(c+4)$と表せる。

2点$(3, \, 0)$、$(3, \, -3)$を両端とする線分と$G$が共有点をもつような$c$の範囲は？

2点$(3, \, 0)$、$(3, \, -3)$を両端とする線分は、$y$軸と平行な$0$から$-3$の線分である。

よって、グラフ$G$が$x=3$のとき$y$の範囲が$-3 \leq y \leq 0$であれば、線分とグラフ$G$は共有点を持つ。

$y=x^2-2(c+2)x+c(c+4)$に$x=3$を代入すると、

$y=3^2-2(c+2)3+c(c+4)$

$y=(c-3)(c+1)$

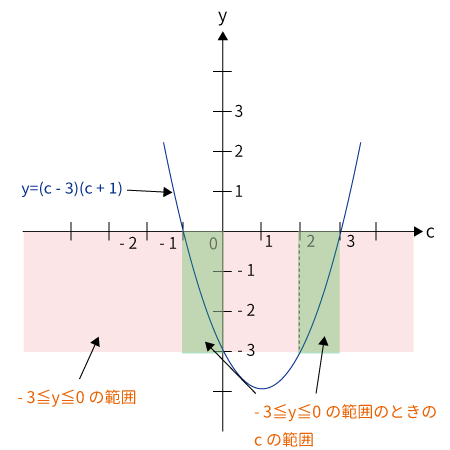
よって、$-3 \leq y =(c-3)(c+1) \leq 0$

グラフで確認すると、この不等式を満たす$c$の範囲は$-1 \leq c \leq 0$、$2 \leq c \leq 3$であると分かった。

第１問 [３]（２）

上記「どれくらい平行移動した？」より、グラフ$G$は$y=x^2$を$x$軸方向に$c+2$、$y$軸方向に$-4$平行移動したグラフということが分かっている。

よって、$c$の値を求めればよい。

$c$を求める

$G$：$y=x^2-2(c+2)x+c(c+4)$が$(3, \, -1)$を通るときなので、$y=x^2-2(c+2)x+c(c+4)$に$x=3, \, y=-1$を代入する

上記「2点$(3, \, 0)$、$(3, \, -3)$を両端とする線分と$G$が共有点をもつような$c$の範囲は？」で$x=3$は代入済で、$y=c^2-2c -3$（因数分解前）である。これに$y=-1$を代入すると、

$-1=c^2-2c -3$

$\displaystyle c=1 \pm \sqrt{3}$となる。$2 \leq c \leq 3$の場合なので、$c=1 + \sqrt{3}$である。

よって、「$y=x^2$を$x$軸方向に$c+2$、$y$軸方向に$-4$平行移動したグラフ」に代入すると、

$x$軸方向に$1 + \sqrt{3}+2=3+\sqrt{3}$、$y$軸方向に$-4$だけ平行移動したものと分かった。

グラフ$G$と$y$軸との交点の$y$座標

このときのグラフ$G$は$y=x^2$を$x$軸方向に$1 + \sqrt{3}+2=3+\sqrt{3}$、$y$軸方向に$-4$だけ平行移動したものなので、平行移動の公式より、

$y-(-4)=\{x-(3+\sqrt{3})\}^2$

$y$軸との交点を求めるので、$x=0$を代入する、

$y-(-4)=\{-(3+\sqrt{3})\}^2$

グラフ$G$と$y$軸との交点の$y$座標$8+6\sqrt{3}$

スポンサーリンク

 

キーワード

気になる人は調べてみてね。

平行移動、グラフ、因数分解、不等式、交点、解の公式、